Méthode des moindres carrés

Résolution d'une équation par la méthode des moindres carrés

Traduisible et imprimable

Le problème

On part d'un nuage de points (quelque chose de nébuleux), un ensemble de points (x, y) enregistrés, qui représentent une courbe plus ou moins irrégulière, voire complètement cahotique.
On cherche à déterminer une courbe lisse, représentée par une équation (qui comporte un nombre donné de paramètres), qui soit aussi proche que possible de ce nuage de points.

L'approche

Il s'agit donc ici de trouver les coefficients (aka paramètres) d'une équation, impliquant un nombre donné (choisi) de paramètres, afin que la courbe qui le représente soit aussi proche que possible d'un ensemble de points donnés.
Autrement dit, que la courbe trouvée colle autant que possible au nuage des points de départ.

Données initiales : Nuage de points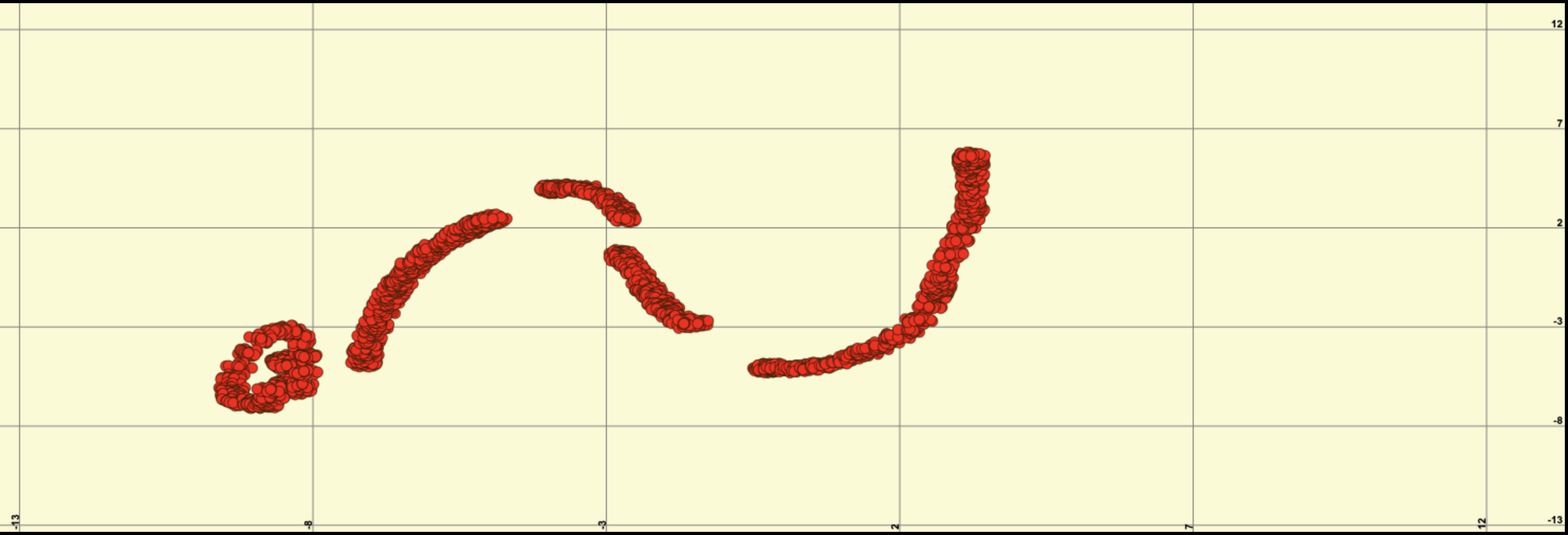

Données finales : Courbe (ici un polynôme de degré 4)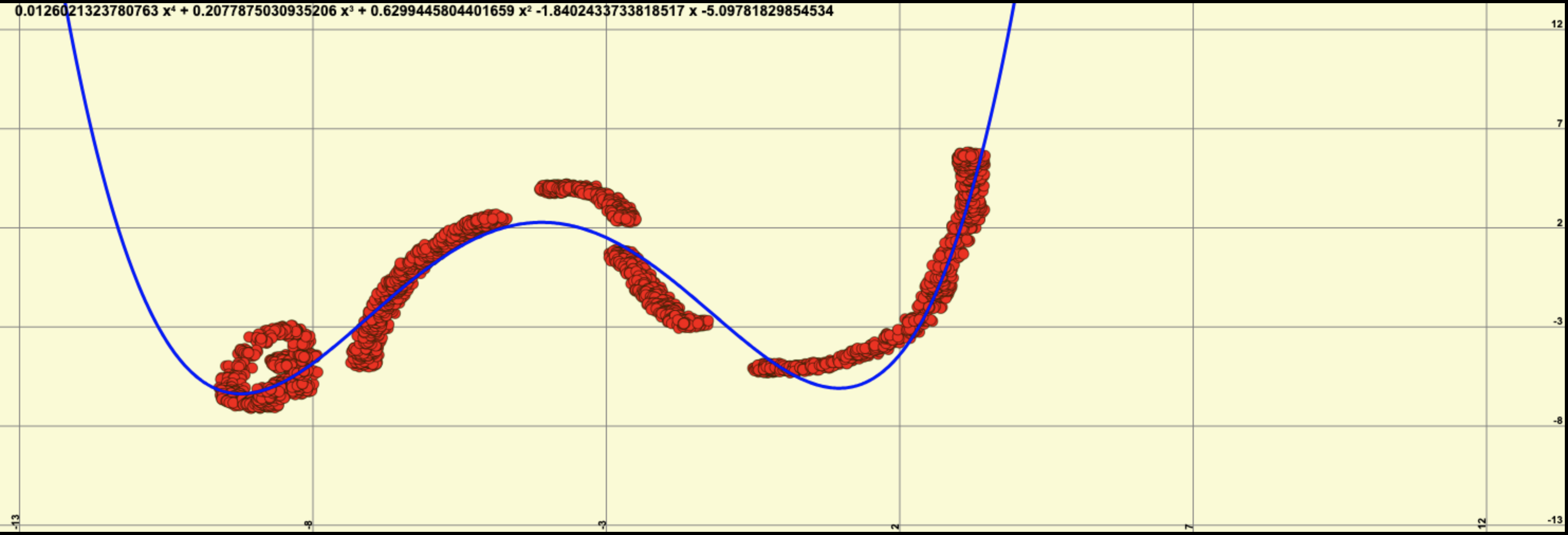
Nuage de points & courbe

Exemple, illustré

La méthode des moindres carrés ne concerne pas que les fonction polynômes, loin de là.
On veut ici déterminer les coefficients d'une courbe polynomiale du second degré, à partir d'un nuage de points enregistrés.
On choisit ici un degré 2 pour simplifier les équations qui suivent.
La résolution d'un polynôme de degré supérieur suivrait le même mode opératoire.

On cherche donc à déterminer les coefficients d'un polynôme du 2^nd degré, dont les éléments sont aussi proches que possible des points d'un ensemble donné (enregistré à bord d'un bateau, dans le cas qui suit).

Les points peuvent être définis (par leurs coordonnés) de différentes manières, par exemple ici un cap compas (HDC, pour HeaDing Compass) et une route fond (COG, pour Course Over Ground) pour déterminer une courbe de déviation, un angle de vent réel et une vitesse du bateau pour déterminer des polaires, etc.

Pour la commodité de la notation, on prendra les points coordonnés génériquement, comme suit :

$$ P^{HDC}_{COG} = P^x_y $$

, écrit aussi

$$ y = f(x) $$

où

$$ f(x) = ax^2 + bx + c $$

Donc, pour tous les points $(x, y)$ du nuage de données enregistrées, on cherche les coefficients a, b, et c d'un polynôme pour lequel

$$ ax^2 + bx + c $$

est le plus proche possible de y, c'est à dire que la différence

$$ ax^2 + bx + c - y $$

soit la plus petite possible, donc, que pour tous les points enregistrés, le carré de cette différence soit le plus proche possible de zéro (on élève au carré pour supprimer le signe, d'où le nom de la méthode), et donc que le cumul de ces différences soit en définitive la plus petite possible.
Ceci revient à calculer les coefficients a, b et c pour lesquels la dérivée première de cette sommation des carrés des différences par rapport à chacun des coefficients a, b et c est nulle, ce qui s'écrit :

$$ ([\Sigma(ax^2 + bx + c - y)^2])' = 0 $$

Pour insister : c'est bien ici le cœur de la méthode.

Pour tous les points du nuage à résoudre, pour chaque x, on calcule la valeur de la fonction (ici polynôme) f(x), et on veut que sa différence avec y soit la plus petite possible.
Donc que la derivée de la fonction de cette différence (au carré, pour supprimer les histoires de signe) soit nulle.

$$ ([\Sigma(ax^2 + bx + c - y)^2])' = 0 $$

s'écrit aussi

$$ ([\Sigma((ax^2 + bx + c - y) \times (ax^2 + bx + c - y))])' = 0 $$

On développe la somme avant de dériver :

$ S = a^2\Sigma x^4 + 2ab\Sigma x^3 + 2ac\Sigma x^2 - 2a\Sigma yx^2 + b^2\Sigma x^2 + 2bc\Sigma x - 2b\Sigma yx + c^2\Sigma x^0 - 2c\Sigma y + \Sigma y^2 $

On dérive l'expression ainsi obtenue

Par rapport à a :
$ \dfrac{\partial S}{\partial a} = 2a\Sigma x^4 + 2b\Sigma x^3 + 2c\Sigma x^2 - 2\Sigma yx^2 = 0 $
Par rapport à b :
$ \dfrac{\partial S}{\partial b} = 2a\Sigma x^3 + 2b\Sigma x^2 + 2c\Sigma x^1 - 2\Sigma yx^1 = 0 $
Par rapport à c :
$ \dfrac{\partial S}{\partial c} = 2a\Sigma x^2 + 2b\Sigma x^1 + 2c\Sigma x^0 - 2\Sigma yx^0 = 0 $

On change les termes en y de côté, on simplifie par 2 :

$ a\Sigma x^4 + b\Sigma x^3 + c\Sigma x^2 = \Sigma yx^2 $
$ a\Sigma x^3 + b\Sigma x^2 + c\Sigma x^1 = \Sigma yx^1 $
$ a\Sigma x^2 + b\Sigma x^1 + c\Sigma x^0 = \Sigma yx^0 $

et on obtient la résolution matricielle suivante :

$ \begin{vmatrix} a & b & c \end{vmatrix} = \begin{vmatrix} \Sigma x^4 & \Sigma x^3 & \Sigma x^2 \\ \Sigma x^3 & \Sigma x^2 & \Sigma x^1 \\ \Sigma x^2 & \Sigma x^1 & \Sigma x^0 \end{vmatrix} ^ {-1} \times \begin{vmatrix} \Sigma yx^2 \\ \Sigma yx^1 \\ \Sigma yx^0 \end{vmatrix} $

Remarques :
- Les termes $ \Sigma x^0 $ représentent le nombre de points dans la courbe à lisser.
- Un polynôme du 2^nd degré a 3 coefficients, la dimension des matrices qu'on gère (carrée, ligne, et colonne) est donc 3.

Pour un polynôme de degré n, le travail à effectuer se "résume" ainsi à inverser la matrice carrée $ \Sigma x^{0->2n} $ et de la multiplier par la matrice colonne $ \Sigma yx^{0->n} $ pour obtenir la matrice ligne des coefficients du polynôme recherché.

Cas d'une courbe de déviation

Précision : qu'est-ce que c'est que ce truc ?
À bord d'un bateau, on a un compas, qui permet de savoir dans quelle direction on se dirige, élément essentiel à la tenue de l'estime.
Le "nord vrai" (géographique) est celui des cartes.
Le "cap magnétique" est celui qui fait intervenir la déclinaison magnétique locale (qui varie suivant l'endroit où on se trouve sur la planète, et la date).
Le "cap compas" est celui indiqué par le compas, qui subit les influences magnétiques du bateau lui-même (métal, équipements électriques, etc).
La déviation est la différence entre le cap compas et le cap magnétique.
Elle dépend du bateau, et de son cap, et est donc une fonction du cap compas lui-même.
Sur un bateau en acier, elle peut atteindre des valeurs énormes - comme 40 degrés - dont il est sans aucun doute de bon ton de tenir compte...

On cherche ici à élaborer une courbe de déviation, à partir de points enregistrés depuis la station NMEA du bord.
Dans ce contexte, la station doit comporter un GPS, et un compas (compas électronique, donc). Le GPS permettra à la station NMEA de générer des chaînes RMC - qui vont contenir la route fond (Course Over Ground, aka COG), le compas fournira à la station ce dont elle a besoin pour générer les Caps Compas (Heading, aka HDG, HDM, etc, suivant les stations).
Le fichier contenant les informations produites par la station NMEA aura ainsi une allure comme celle-ci :

    . . .
    $IIRMC,190402,A,0854.980,S,14006.028,W,00.0,008,031110,10,E,A*07
    $IIVHW,,,126,M,00.0,N,,*61
    $IIVLW,02839,N,000.0,N*53
    $IIVWR,027,R,07.2,N,,,,*61
    $IIDPT,012.3,+0.7,*40
    $IIGLL,0854.979,S,14006.029,W,190403,A,A*56
    $IIHDG,126,,,10,E*16
    . . .

On note que le fichier peut contenir d'autres données (VHW, DPT, GLL, VLW, etc), qu'on ignorera ici.
Ce fichier sera ensuite travaillé pour produire un document où ne figureront que les données qui nous concernent ici, à savoir la déviation en fonction du cap.
Par exemple (en JSON ici) :

    [
        { "hdc": 210.000000, "dev": 4.000000 },
        { "hdc": 210.000000, "dev": 4.000000 },
        { "hdc": 210.000000, "dev": -1.000000 },
        { "hdc": 210.000000, "dev": -2.000000 },
        { "hdc": 208.000000, "dev": -4.000000 },
        . . .
    ]

Plus de détails sur ces opérations sont disponibles dans d'autres documents :

On considère donc que la forme générique d'une courbe de déviation est

$$ dev = a + (b \times \cos r) + (c \times \cos r) + (d \times \sin 2r) + (e \times \cos 2r) $$

ce qui n'est manifestement pas un polynôme, mais comme ce sont les coefficients de la formule qu'on cherche, la méthode des moindres carrés peut s'appliquer.
Dans l'équation ci-dessus, r est le Cap Compas, dev est la déviation (δ entre HDC et HDM, cap compas et cap magnétique).
On cherche donc à définir une fonction f pour laquelle la déviation dev est obtenue en fournissant r:

$$ dev = f(r) $$

Grâce au logging, on dispose d'un nuage de points qui comportent chacun au moins les informations suivantes :

HDC (Heading Compass)
COG (Course Over Ground)

Le logging doit s'effectuer sans courant, et sans dérive, de façon à être sûr que la différence entre le cap compas HDC (corrigé de la déclinaison locale) et la route fond (COG) est bien la déviation d, que l'on cherche. Pas de dérive, pas de courant, la route fond est égale à la route surface, qui est égale au cap vrai du bateau.
Les éléments du nuage de points dont on dispose (élaboré à partir du logging) sont définis en

$$ P_{d}^{HDC} = P_{d}^{r} = P_{y}^{x} $$

En abscisse le Cap Compas, en ordonnée la déviation.
On cherche les valeurs de 5 coefficients :

$ \begin{vmatrix} a & b & c & d & e \end{vmatrix} $

La dimension des matrices à gérer est donc cette fois-ci 5. On applique la méthode des moindres carrés, décrite ci-dessus.
On obtient les coefficients $ \begin{vmatrix} a & b & c & d & e \end{vmatrix} $ en résolvant :

$ \begin{vmatrix} a & b & c & d & e \end{vmatrix} = \begin{vmatrix} &n &\sum_{i=0}^{n}\sin(r) &\sum_{i=0}^{n}\cos(r) &\sum_{i=0}^{n}\sin(2r) &\sum_{i=0}^{n}\cos(2r) \\ &\sum_{i=0}^{n}\sin(r) &\sum_{i=0}^{n}\sin(r)^2 &\sum_{i=0}^{n}\sin(r)cos(r) &\sum_{i=0}^{n}\sin(2r)sin(r)) &\sum_{i=0}^{n}\cos(2r)sin(r) \\ &\sum_{i=0}^{n}\cos(r) &\sum_{i=0}^{n}\cos(r)sin(r) &\sum_{i=0}^{n}\cos(r)^2 & \sum_{i=0}^{n}\sin(2r)cos(r) &\sum_{i=0}^{n}\cos(2r)cos(r) \\ &\sum_{i=0}^{n}\sin(2r) &\sum_{i=0}^{n}\sin(2r)sin(r) &\sum_{i=0}^{n}\sin(2r)cos(r) &\sum_{i=0}^{n}\sin(2r)^2 &\sum_{i=0}^{n}\cos(2r)sin(2r) \\ &\sum_{i=0}^{n}\cos(2r) &\sum_{i=0}^{n}\cos(2r)sin(r) &\sum_{i=0}^{n}\cos(2r)cos(r) &\sum_{i=0}^{n}\cos(2r)sin(2r) &\sum_{i=0}^{n}\cos(2r)^2 \end{vmatrix} ^{-1} \times \begin{vmatrix} &\sum_{i=0}^{n}\ dev \\ &\sum_{i=0}^{n}\ dev.sin(r) \\ &\sum_{i=0}^{n}\ dev.cos(r) \\ &\sum_{i=0}^{n}\ dev.sin(2r) \\ &\sum_{i=0}^{n}\ dev.cos(2r) \end{vmatrix} $

Fastoche !

Pour plus de détails, voir aussi ce document, et aussi celui-ci, pour un exemple complet (incluant le code pour la résolution des matrices), partant du fichier de log, passant par le calcul des coefficients, et aboutissant à l'affichage de la courbe de déviation, avec une interface Web.

Solving an Equation Using the Least Squares Method

Translatable and printable

The problem

We start with a point cloud (something nebulous), a set of recorded points (x, y) that represent a more or less irregular, or even completely chaotic, curve.
We want to determine a smooth curve, represented by an equation (which has a given number of parameters), that is as close as possible to this point cloud.

The Approach

The goal here is to find the coefficients (also known as parameters) of an equation, involving a given (chosen) number of parameters, so that the curve representing it is as close as possible to a given set of points.
In other words, the resulting curve should fit the initial point cloud as closely as possible.

Initial Data: Cloud of Points
Nuage de points

Final data: Curve (here a polynomial of degree 4)
Nuage de points & courbe

Illustrated Example

The least squares method is not limited to polynomial functions, far from it.
Here, we want to determine the coefficients of a quadratic polynomial curve from a set of recorded points.
We choose a degree 2 polynomial to simplify the following equations.
Solving a higher-degree polynomial would follow the same procedure.

We therefore seek to determine the coefficients of a quadratic polynomial whose elements are as close as possible to the points of a given set (recorded on board a boat, in the following case).

The points can be defined (by their coordinates) in different ways, for example, here a compass heading (HDC) and a course over ground (COG) to determine a deviation curve, a true wind angle and boat speed to determine polars, etc.

For the sake of notation, we will take the coordinate points generically, as follows:

$$ P^{HDC}_{COG} = P^x_y $$

, also written

$$ y = f(x) $$

$$ f(x) = ax^2 + bx + c $$

herefore, for all points (x,y) in the recorded data cloud, we are looking for the coefficients a, b, and c of a polynomial for which

$$ ax^2 + bx + c $$

is as close as possible to y, that is to say that the difference

$$ ax^2 + bx + c - y $$

this difference should be as small as possible, meaning that for all recorded points, the square of this difference should be as close to zero as possible (squaring removes the sign, hence the name of the method), and therefore the sum of these differences should ultimately be as small as possible.
This amounts to calculating the coefficients a, b, and c for which the first derivative of this summation of the squares of the differences with respect to each of the coefficients a, b, and c is zero, which can be written as:

$$ ([\Sigma(ax^2 + bx + c - y)^2])' = 0 $$

To emphasize: this is the core of the method.

For all the points in the cloud to be solved, for each x, we calculate the value of the function (here a polynomial) f(x), and we want its difference with y to be as small as possible.
Therefore, we want the derivative of the function of this difference (squared, to eliminate any sign issues) to be zero.

$$ ([\Sigma(ax^2 + bx + c - y)^2])' = 0 $$

can be also written

$$ ([\Sigma((ax^2 + bx + c - y) \times (ax^2 + bx + c - y))])' = 0 $$

We expand the sum before differentiating:

$ S = a^2\Sigma x^4 + 2ab\Sigma x^3 + 2ac\Sigma x^2 - 2a\Sigma yx^2 + b^2\Sigma x^2 + 2bc\Sigma x - 2b\Sigma yx + c^2\Sigma x^0 - 2c\Sigma y + \Sigma y^2 $

We derive the expression thus obtained

Compared to a:
$ \dfrac{\partial S}{\partial a} = 2a\Sigma x^4 + 2b\Sigma x^3 + 2c\Sigma x^2 - 2\Sigma yx^2 = 0 $
Compared to b:
$ \dfrac{\partial S}{\partial b} = 2a\Sigma x^3 + 2b\Sigma x^2 + 2c\Sigma x^1 - 2\Sigma yx^1 = 0 $
Compared to c:
$ \dfrac{\partial S}{\partial c} = 2a\Sigma x^2 + 2b\Sigma x^1 + 2c\Sigma x^0 - 2\Sigma yx^0 = 0 $

We swap the y-terms, we simplify by 2:

$ a\Sigma x^4 + b\Sigma x^3 + c\Sigma x^2 = \Sigma yx^2 $
$ a\Sigma x^3 + b\Sigma x^2 + c\Sigma x^1 = \Sigma yx^1 $
$ a\Sigma x^2 + b\Sigma x^1 + c\Sigma x^0 = \Sigma yx^0 $

and we obtain the following matrix resolution:

Notes :
- The terms $ \Sigma x^0 $ epresent the number of points on the curve to be smoothed.
- A quadratic polynomial has 3 coefficients, so the dimension of the matrices we are working with (square, row, and column) is 3.

For a polynomial of degree n, the work to be done essentially involves inverting the square matrix $ \Sigma x^{0->2n} $ and multiplying it by the column matrix $ \Sigma yx^{0->n} $ to obtain the row matrix of coefficients of the desired polynomial.

Case of a deviation curve

Clarification: What exactly is this thing?
On board a boat, you have a compass, which allows you to know which direction you're heading, an essential element for dead reckoning.
"True north" (geographic north) is the north shown on the charts.
"Magnetic heading" takes into account the local magnetic declination (which varies depending on your location on the planet and the date).
"Compass heading" is the one indicated by the compass, which is affected by the magnetic influences of the boat itself (metal, electrical equipment, etc.).
Deviation is the difference between the compass heading and the magnetic heading.
It depends on the boat and its heading, and is therefore a function of the compass heading itself.
On a steel boat, it can reach enormous values—like 40 degrees—which it's definitely wise to take into account...

The goal here is to develop a deviation curve from points recorded by the onboard NMEA station.
DIn this context, the station must include a GPS and a compass (an electronic compass). The GPS will allow the NMEA station to generate RMC strings, which will contain the course over ground (COG). The compass will provide the station with what it needs to generate compass headings (HDG, HDM, etc., depending on the station).
The file containing the information produced by the NMEA station will thus look like this:

    . . .
    $IIRMC,190402,A,0854.980,S,14006.028,W,00.0,008,031110,10,E,A*07
    $IIVHW,,,126,M,00.0,N,,*61
    $IIVLW,02839,N,000.0,N*53
    $IIVWR,027,R,07.2,N,,,,*61
    $IIDPT,012.3,+0.7,*40
    $IIGLL,0854.979,S,14006.029,W,190403,A,A*56
    $IIHDG,126,,,10,E*16
    . . .

Note that the file may contain other data (VHW, DPT, GLL, VLW, etc.), which we will ignore here.
This file will then be processed to produce a document containing only the data relevant to our purpose, namely the deviation as a function of heading.
For example (in JSON here) :

    [
        { "hdc": 210.000000, "dev": 4.000000 },
        { "hdc": 210.000000, "dev": 4.000000 },
        { "hdc": 210.000000, "dev": -1.000000 },
        { "hdc": 210.000000, "dev": -2.000000 },
        { "hdc": 208.000000, "dev": -4.000000 },
        . . .
    ]

More details on these operations are available in other documents:

Therefore, the generic form of a deviation curve is considered to be

$$ dev = a + (b \times \cos r) + (c \times \cos r) + (d \times \sin 2r) + (e \times \cos 2r) $$

This is clearly not a polynomial, but since we are looking for the coefficients of the formula, the least squares method can be applied.
In the equation above, r is the compass heading, and dev is the deviation (δ between HDC and HDM, compass heading and magnetic heading).
We therefore seek to define a function f for which the deviation dev is obtained by providing r:

$$ dev = f(r) $$

Thanks to logging, we have a point cloud, each point containing at least the following information:

HDC (Heading Compass)
COG (Course Over Ground)

Logging must be performed without current or drift to ensure that the difference between the compass heading (corrected for local declination) and the course over ground (COG) is indeed the deviation d we are looking for. With no drift and no current, the course over ground equals the course through the water, which is equal to the boat's true heading.
The elements of the available point cloud (generated from the logging) are defined in

$$ P_{d}^{HDC} = P_{d}^{r} = P_{y}^{x} $$

The x-axis represents the compass heading, and the y-axis represents the deviation.
We are looking for the values of 5 coefficients:

$ \begin{vmatrix} a & b & c & d & e \end{vmatrix} $

The dimension of the matrices to be managed is therefore 5 this time. We apply the least squares method, described above.
The coefficients $ \begin{vmatrix} a & b & c & d & e \end{vmatrix} $ are obtained by solving:

Easy peasy!

For more details, see also this document, and also this one, for a complete example (including the code for solving the matrices), starting from the log file, through the calculation of the coefficients, and ending with the display of the deviation curve, with a Web interface.