The following document is designed to be visualized from a web browser, or printed from it (a pdf can also be generated from the page).
The printed version will have page breaks and other formattings that will not be displayed from the web browser.
Likewise, the web version has links that would be meaningless in a printed document.
When printing, you will have the possibility - from the dialog showing up in the browser - to hide or show different
data like headers, footers, page numbers, etc, and even scale.
But, I'm still looking for a (free) way to generate the page numbers in the table of contents...
Le document qui suit est conçu pour être visualisé dans un navigateur web, ou imprimé à partir de celui-ci (on peut aussi générer un pdf).
La version imprimée comporte des sauts de page et autres formattages qui ne seront pas visibles à partir du navigateur.
De même, la version web comporte des liens qui n'auraient guère de sens dans un document imprimé.
Lors de l'impression, vous aurez la possibilité - à partir des boites de dialogue du navigateur - de faire apparaître ou pas
des données comme les en-têtes et bas de page, numéros de page, etc, et même l'échelle.
Mais, je suis toujours en train de chercher comment générer (gratuitement) les numéros de page dans la table des matières...
Il s'agit de pouvoir continuer à naviguer sereinement - à savoir où on est, à savoir où on va, et à savoir ce qu'il faut faire pour aller là où on veut aller - même quand les batteries sont à plat, et que les piles sont mortes.
Et ce même si il fait nuit, qu'on est au près, que la météo répète qu'il y a un avis de coup de vent (qu'on n'entend pas, puisque les piles sont mortes, disais-je), qu'il va bientôt neiger, et que tout le monde a la gerbe.
C'est de toute évidence de la pure fiction, mais on a le droit d'y croire, et on y croit !
Le monde a été découvert à la voile, sans électricité, les techniques à mettre en œuvre sont d'autant mieux connues qu'elles ont longtemps été les seules disponibles. Un des objectifs de ce document est aussi de les préserver, de ne pas les laisser s'oublier, de ne pas les perdre, ce serait vraiment trop bête.
D'autant que la sécurité en mer - comme ailleurs - échappe totalement à la mode et à l'actualité.
On évoquera ici des outils et les techniques qui permettent de les mettre en œuvre, tant en ce qui concerne leur utilisation que la façon d'exploiter les données qu'ils mesurent.
Par contre, on passera rapidement sur la façon d'utiliser un compas de relèvement, on ne parlera guère de la façon dont on se sert d'un sextant... Ce document est plus un aide-mémoire quant à la manière d'effectuer les divers calculs qui découlent de l'utilisation des instruments de navigation.
Donc :
Avant de disposer d'aides électroniques à la navigation, on naviguait à l'estime.
Le principe de la navigation à l'estime est le suivant :
On part d'un point connu, et on tâche de tenir compte de tous les facteurs qui déplacent le navire, comme sa vitesse et son cap,
sa dérive, le courant, etc. Ceci permet d'obtenir une position estimée à n'importe quel moment.
À chaque fois que c'est possible, on recale son estime en faisant un point. En fonction de l'endroit où on se trouve, à savoir en vue ou hors de vue des côtes, les méthodes de point seront différentes, et évoquées plus avant dans ce document.
Pour faire court, la clef d'une estime correcte tient en deux points :
Pour tenir son estime, il faut pouvoir :
Pour mesurer la distance parcourue, on a longtemps mesuré la vitesse du bateau, et calculé la distance parcourue d'après le temps passé à une vitesse donnée, ce qui implique de pouvoir aussi mesurer le temps.
On verra - notamment dans la section dédiée à la navigation astronomique - que la mesure du temps est un problème critique et important, non pas tant pour la tenue de l'estime, que pour la recaler.
On peut répartir les différents instruments de navigation en plusieurs catégories :
De plus, quand ce n'est pas l'outil qui décide, son utilisateur doit savoir ce qu'il fait, anticiper la valeur des mesures qu'il fait, et des résultats qu'il trouve. Cette attitude décisive permet aussi de détecter rapidement les erreurs et les aberrations, qui ne manqueront pas d'arriver.
Rien de nouveau ici. Tous les instruments mentionnés ici sont connus depuis au moins cent ans.
Certains peuvent être construits avec les moyens du bord. D'autres non.
Il demeure cependant probablement intéressant de mentionner de quels instruments il s'agit.
Allons-y.
Et puisqu'on en est à parler anglais, "estime" en anglais se dit "dead reckoning"...
Le verbe "to reckon" signifie "estimer". Jusque là tout va bien. Mais pourquoi "dead", qui signifie "mort" ?
Qu'est ce que pourrait bien être une "estime morte" ?
Renseignements pris, ce "dead" devrait s'écrire "ded", qui est une abbréviation de "deduction".
"Dead Reckoning" signifie donc "Estime par déduction". C'est beaucoup mieux.
Le loch à bateau est une bûche, un peu plus élaborée.
Il est fait essentiellement d'une planche de bois - c'est elle le bateau, celle qu'on appelle le bateau du loch - à
laquelle est amarrée une ligne par une patte d'oie, de façon à ce qu'elle flotte verticalement.
La ligne comporte des nœuds à intervalles réguliers de 15,43 mètres. Elle est en général enroulée sur un touret.
Le principe de fonctionnement est le suivant : on mouille le loch en même temps qu'on retourne un sablier de 30 secondes,
et on laisse filer la ligne de son touret jusqu'à ce que tout le sable soit écoulé, après quoi on compte les nœuds
qui sont passés à l'eau, et on remonte le tout à bord.
30 secondes constituent la 120e partie d'une heure, 15,43 mètres la 120e partie d'un mille marin (de 1852 mètres).
C'est ainsi qu'on "file cinq nœuds et demi", et non pas qu'on "avance à cinq milles et demi à l'heure".
On a tous déjà entendu "cinq nœuds à l'heure". Pas de commentaire !..
Le loch à poisson est un instrument mécanique, plus élaboré, qui présente cet avantage d'enregistrer la distance parcourue.
Probablement inventé en Chine. C'est ce que les terriens appellent une boussole.
On utilise des compas de route, et des compas de relèvement.
Le compas de route est fixé au bateau, et posé dans l'axe de la "ligne de foi".
Le compas de relèvement se tient à la main.
Les compas magnétiques sont basés sur le champ magnétique terrestre.
Ils indiquent le nord (à l'inverse du compas chinois, qui indique le sud) magnétique, qui se déplace avec le temps, et qui n'est pas situé au même endroit que le nord géographique,
qui est celui des cartes.
Le cap compas fait l'objet de deux corrections pour restituer le cap vrai (cap géographique),
celui qui s'exprime par rapport au nord de la carte. On verra à ce sujet la section Tenue de l’Estime.
Le compas de relèvement est utilisé pour connaître l'angle que fait un amer vu du bateau avec le nord magnétique.
La correction de déviation n'est pas appliquée au compas de relèvement, on considère (parfois à tort) qu'il n'est pas sujet
aux masses magnétiques qui engendrent la déviation appliquée au compas de route. Les bateaux - en général des navires - pour
lesquels c'est faux utilisent plutôt un cercle de gisements. Le gisement est l'angle que fait un amer avec l'axe du bateau.
On aura le relèvement de l'amer en faisant intervenir le cap du bateau, et les corrections (déclinaison et déviation) qui s'imposent.
Les compas gyroscopiques ne sont pas sujets à ce genre de phénomènes magnétiques, mais ils consomment beaucoup d'énergie.
Les compas étaient autrefois divisés en 32 parties (le compas chinois est divisé en 24 parties) égales appelées "quarts" ; ils sont maintenant
gradués en degrés, de 0° à 360°, dans le sens des aiguilles d'une montre, le nord à 0°, l'est à 90°, le sud à 180° et l'ouest à 270°.
La carte est le plus important de tous les instruments de navigation.
De nombreux logiciels fournissent maintenant des cartes électroniques.
Les cartes en papier présentent cet inconvénient d'être chères et fragiles.
Elles présentent néanmoins l'avantage incontestable de ne jamais tomber en panne.
Moyennant le fait qu'on sait ce qu'on veut mesurer en matière d'angle, le plus simple des rapporteurs sera suffisant, pourvu qu'il soit gradué en degrés. Certains, plus élaborés, seront plus pratiques. D'autres, plus sophistiqués, seront superflus.
Les Anglo-saxons utilisent des "règles parallèles", les autres des rapporteurs, plus ou moins élaborés. Il n'y a pas lieu de polémiquer, mais les règles parallèles sont faites comme s'il était difficile de mesurer un angle avec un rapporteur...
De la même manière, parmi ceux qui utilisent des rapporteurs, on voit fréquemment surgir des multitudes d'accessoires alambiqués qui tournent, pivotent et galipettent, comme pour s'adresser à des utilisateurs qui ne savent pas ce que c'est que l'angle qu'ils mesurent.
Il faut savoir ce qu'on mesure, moyennant quoi - disais -je - un rapporteur est amplement suffisant.
La "Règle de Cras" est son avatar le plus élaboré,
et fournit toutes les fonctionnalités qu'on est en droit d'attendre d'un tel outil, avec des risques d'erreur de manipulation minimes.
Les soi-disant recherches dans ce domaine sont vaines, la clef de voûte,
c'est les compétences de l'utilisateur. Au lieu d'essayer d'inventer de nouveaux rapporteurs,
il semble plus judicieux d'apprendre à se servir de ceux qui existent, ils ont en général fait leurs preuves.
Il ne s'agit que de mesurer des angles, en degrés, allant de zéro à trois cent soixante.
Si on tient la carte correctement (Il y a des cartes pour lesquelles ce n'est pas vrai. Je sais), le 0 et le 360 sont en haut,
90 à droite, 180 en bas, et 270 à gauche.
Celui qui cherche à mesurer un angle qui part du bas à gauche de la carte et va vers le haut à droite, et qui trouve quelque chose comme 210 présente au moins une des pathologies suivantes:
Le compas à pointes sèches est utilisé pour reporter des distances, de la carte sur l'échelle des distances, et vice-versa.
Il est pratique de disposer d'un modèle manœuvrable d'une seule main, pour l'ouvrir comme pour le fermer.
À propos des distances, on utilise le mille marin parce qu'il est défini comme étant la représentation d'une minute d'arc prise au centre de la Terre,
et projetée à sa surface. C'est donc en toute rigueur un angle, et non pas une distance, et de fait, la longueur du mille marin est en moyenne de 1852 mètres, mais varie, entre 1843 et 1862 mètres,
en fonction du diamètre de la Terre, qui n'est pas parfaitement sphérique.
Tous les méridiens ont la même longueur, à l'inverse des parallèles. On mesurera donc les distances sur les méridiens, à savoir sur les côtés verticaux
(lorsqu'il s'agit d’une projection de Mercator, laquelle est orthogonale, à l'inverse des projections de Lambert, gnomoniques et autres) de la carte.
En fonction de la projection utilisée sur la carte (Mercator, Lambert, Gnomonique, etc), les échelles diffèrent. Sur une carte Mercator - par exemple - l'unité de longitude se dilate avec la latitude. Plus la latitude est haute, plus la représentation d'un angle donné est grande, à tel point qu'elle est infinie au pôle. Il convient donc dans ce cas de se référer à l'échelle des distances à une latitude voisine de l'endroit où se trouve la distance à mesurer. Voir à ce sujet la section Mercator et Latitude Croissante.
Dans les films de sous-marins, là où les inondations déclenchent des incendies, on voit les navigateurs faire avec les pointes-sèches des figures qui s'apparentent au patinage artistique, je n'ai absolument aucune idée de ce qu'il peuvent bien faire...
Sabliers, chronomètres, précision requise.
C'est le point le plus sensible au large, qui a de tout temps posé le plus gros problème ; lequel persiste dans notre cas, qui est de naviguer sans électricité.
En vue des côtes, un réveil ou une montre suffit. Il est nécessaire d'avoir l'heure pour consulter les tables de marée, et pour la tenue de l'estime. La précision de la minute - voire de quelques minutes - est suffisante, et on peut l'attendre de la montre qu'on utilise tous les jours.
Au large, on ne dispose que de l'estime et de la navigation astronomique pour avoir un point. La précision devient ici cruciale, quatre secondes d'erreur sur le chronomètre se traduisent par une erreur d'une minute de longitude (à savoir un mille à l'équateur). C'est énorme, et ça va vite.
Il existait jusqu'en 1907 (date à laquelle elles ont cessé d'être publiées) des tables permettant de recaler les chronomètres en mesurant - lorsque c'était possible - la distance lune-soleil avec le sextant. Ces tables ne sont plus publiées, mais les calculs qui permettent de les élaborer sont toujours connus. C'est là que l'informatique peut s'avérer un outil précieux, on peut publier ces tables avant de partir, au même titre que les almanachs et éphémérides. On y reviendra plus en détail.
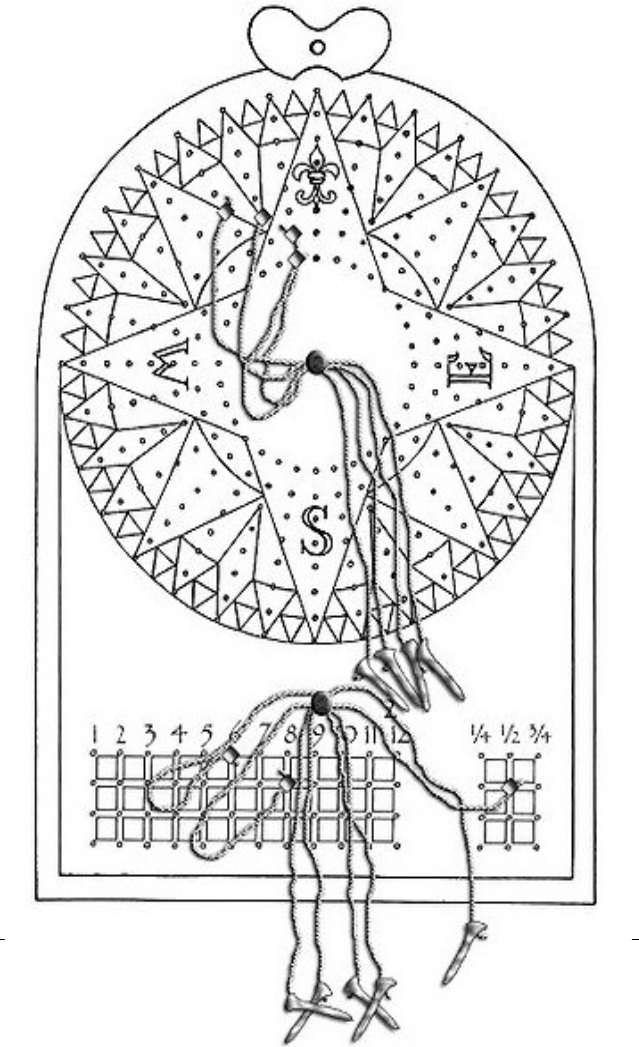
Le renard est un instrument en bois, autrefois utilisé pour la tenue de l'estime, et qui mériterait sans doute de ne pas être oublié.
Sur la figure, on peut voir une rose de compas, divisée en trente-deux quarts (le quart est ici la trente-deuxième partie d'un cercle).
Chaque quart est percé de huit trous, dans lesquels on peut ficher une cheville.
La partie inférieure du renard comporte un tableau, percé de trous pour les chevilles lui aussi.
Voici comment on s'en sert :
Au début de son quart de quatre heures, l'homme de barre s'assure que le renard est vide, toutes les chevilles ont été retirées par le navigateur,
comme on le verra ensuite. Il dispose de huit ficelles, chacune d'elles a une
cheville attachée à ses deux extrémités.
Il regarde son cap, et connaît sa vitesse. Sur le premier cercle disponible à partir de l'intérieur,
il fiche une cheville dans le quart dans lequel il gouverne, et la cheville à l'autre extrémité de la ficelle
va quant à elle dans le tableau du bas, pour indiquer la vitesse courante du navire.
Il procède de même toutes les demi-heures, son quart de quatre heures comportera huit demi-heures,
utilisant à chaque fois un cercle plus éloigné du centre du renard que la fois précédente,
la dernière cheville sera fichée sur le cercle le plus à l'extérieur de la rose du renard.
à la fin du quart, le navigateur vient consulter le renard, et connaît ainsi de demi-heure en demi-heure le cap et la vitesse du
bateau durant les quatre dernières heures, qu'il consigne dans le livre de bord avant de retirer les chevilles du renard.
La tenue de l'estime en découle naturellement.
Le temps était en général mesuré à l'aide d'un sablier (qu'on appelait souvent "ampoulette") d'une demi-heure.
Ceux qui avaient envie d'écourter leur quart (ce "quart"-là fait donc quatre heures... Ah c'est pratique !) retournaient le sablier avant qu'il soit vide. Ils appelaient ça "manger du sable"...
Le livre de bord est un document tenu et mis à jour par le navigateur.
On y consigne tous les éléments nécessaires à la tenue de l'estime, ainsi que les éléments susceptibles d'interférer avec le comportement du navire et
d'influer sur sa marche.
On y notera l'heure et la date, le cap (un seul cap suffit, les autres en découlent, ils seraient redondants), la valeur du loch (à défaut, la vitesse du bateau).
L'état de la mer va impacter la dérive, il sera noté aussi.
Dans la même veine, les conditions météorologiques vont influer sur la marche du bateau, il est opportun de noter la force et la direction du vent,
la valeur indiquée par le baromètre, la visibilité, et le type de nuages observés. Ces informations météorologiques vont permettre le cas échéant d'anticiper
le passage ou l'évolution d'une perturbation.
Le livre de bord doit contenir tout ce qui peut permettre de retracer la route du bateau depuis son point de départ.
Pour s'acquitter de cette fonction, le plus simple des cahiers suffit amplement. On y reviendra.
La tenue du livre de bord va de paire avec le tracé de la route sur la carte, où les points seront portés, assortis de l'heure, et le cas échéant de la valeur du loch.
Indispensable au large.
Très utile près des côtes (tout le monde ne le sait pas !). Dans ce cas, il faut aussi disposer
d'un compas (compas-crayon) pour tracer des cercles, on y reviendra quand on parlera d'arcs capables.
Le sextant sert - lui aussi - à mesurer des angles. Il peut le faire avec une précision de l'ordre de la minute d'arc, ce qui est très fin. Le sextant est un instrument de précision avec lequel il faut être soigneux.
Hors de vue des côtes, il sera utilisé pour observer des astres (soleil, lune, planètes, étoiles).
On observe en fait dans ce cas l'angle que fait un astre avec l'horizon (ipso-facto, pour utiliser le sextant dans ces conditions,
il faut voir l'astre et l'horizon. Ça a l'air idiot, mais la nuit, on peut voir plein d'astres, mais pas toujours l'horizon de manière assez nette).
Cette angle mesuré au sextant est un des paramètres des calculs de la navigation astronomique,
évoquée plus loin. La mesure doit être effectuée avec une précision de l'ordre de la minute d'arc, une erreur d'une minute d'arc a pour conséquence une
erreur d'un mille sur la carte, puisque c'est la définition du mille marin, et que c'est pour ça qu'on l'utilise.
C'est une minute d'arc au centre de la terre, projetée à sa surface (on répète : Le mille est donc un angle, pas une distance. En fonction du diamètre de
la Terre - qui n'est pas constant - en moyenne 1852 mètres, sa longueur varie entre 1843 et 1862 mètres).
Pour avoir un ordre de grandeur de la précision requise, si on tend son bras devant soi :
Le sextant utilise un jeu de deux miroirs pour déterminer l'angle entre deux directions, typiquement l'angle entre la direction dans laquelle on voit un astre, et la direction dans laquelle on voit l'horizon.
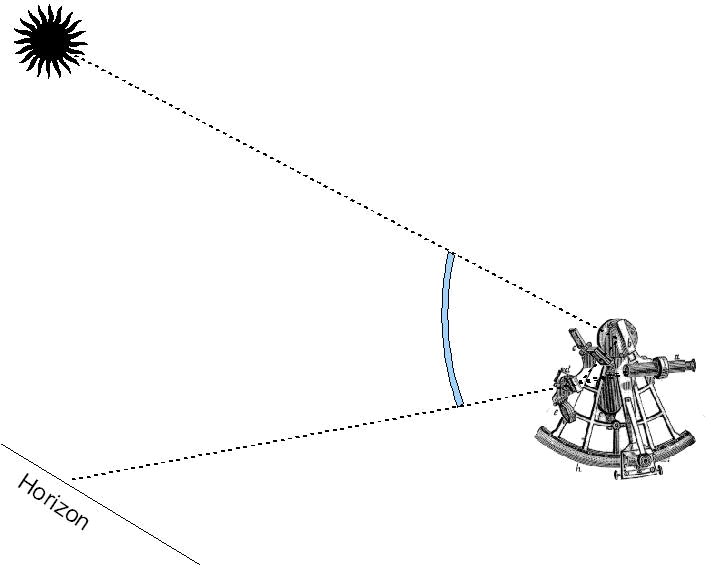
Le fait qu'on utilise un miroir pour amener l'image du soleil sur l'horizon a pour effet de doubler l'angle de l'alidade (partie mobile du sextant, sur laquelle est fixé le grand miroir). Ainsi, pour une hauteur de 90°, l'alidade fera avec sa position originale (0°) un angle de 45°, soit la huitième partie d'un cercle. On s'est longtemps contenté d'octants (octant ⇒ huit). Le sextant représente la sixième partie d'un cercle, soit 60°, on peut ainsi mesurer des angles de 0 à 120 degrés. Bien évidemment, ceci est superflu pour les hauteurs (au-dessus de 90°, retournez-vous, vous avez l'astre dans le dos, andouille), mais ça peut être utile pour les arcs capables, et pour mesurer des distances lune-soleil.
Voilà ce qu'on voit dans la lunette du sextant, à gauche l'horizon, à droite le miroir :
On peut utiliser le sextant en le tenant horizontalement pour observer ou aligner deux amers. Par exemple, en vue de cette côte :
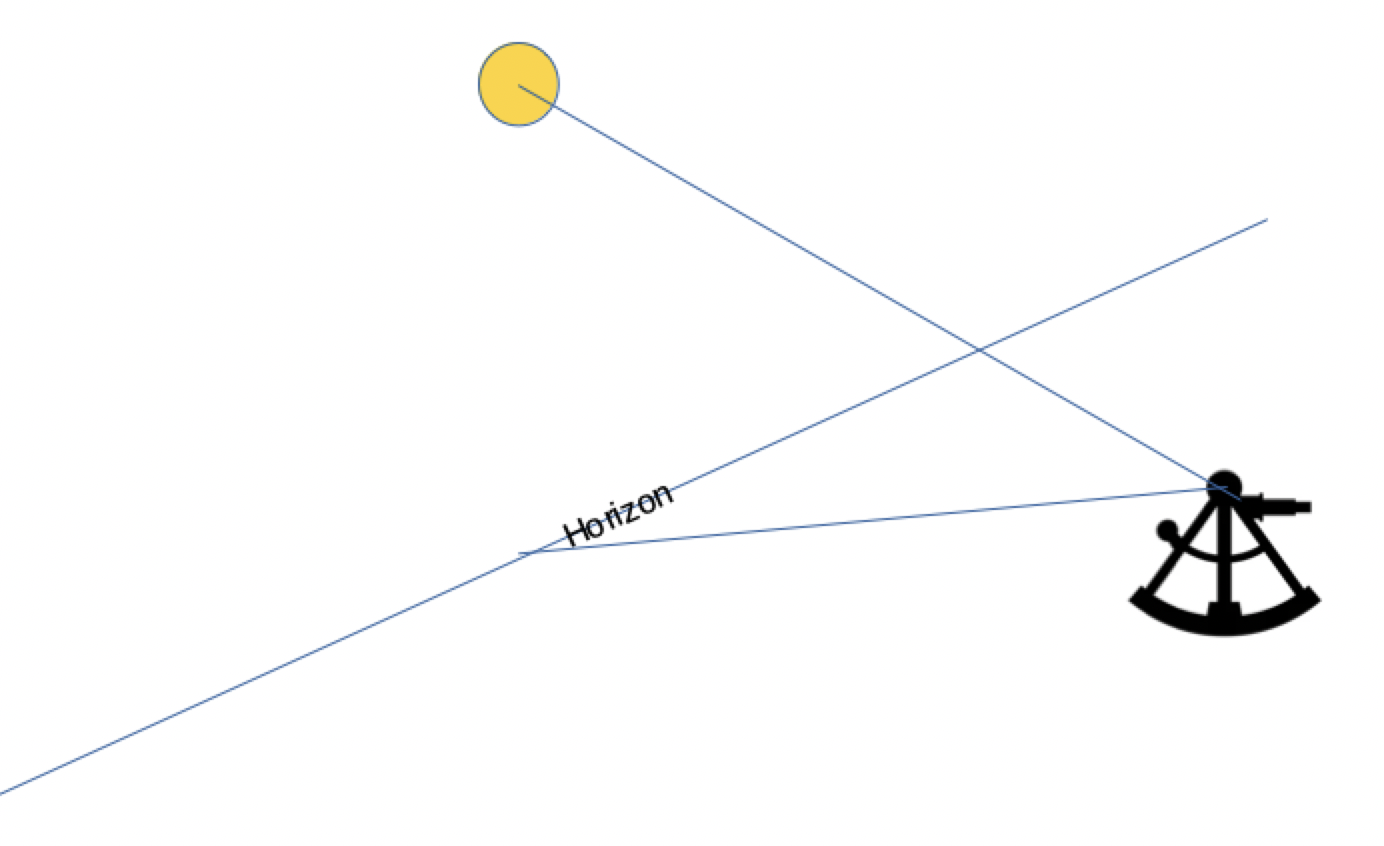
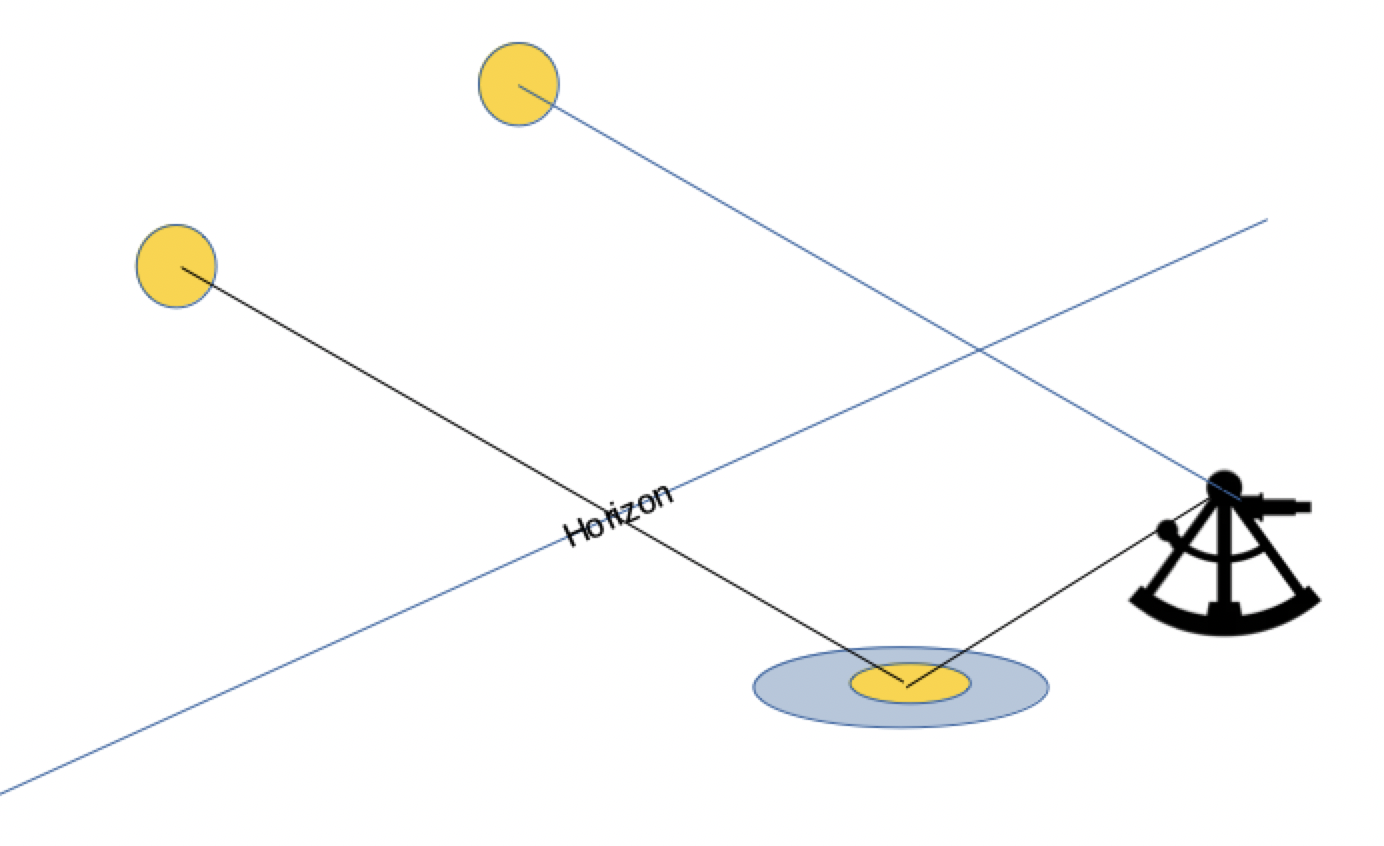
Nous parlons ici des documents qu'occultent les outils électroniques et informatiques.
Les tables et les abaques servent à minimiser le nombre des étapes d'un calcul, les almanachs à en fournir les paramètres.
Les tables et abaques sont des documents permanents, les éphémérides et almanachs sont datés, et donc périssables,
ces derniers sont en général publiés tous les ans.
Tous sont conçus pour que les calculs auxquels ils participent puissent être faits à la main, avec un papier et un crayon.
Élaboration des éphémérides et des almanachs.
Pas à la main, les calculs sont énormes, tant pour les tables de marée que pour les éphémérides astronomiques.
C'est là qu'on reparle d'informatique. Il est simple de confier ce genre de calculs à un ordinateur,
de façon à calculer et publier ces almanachs à terre, avant de partir.
Tout le reste !
On verra dans les sections suivantes les différents calculs à entreprendre.
Les plus complexes sont ceux destinés à la navigation astronomique. On verra qu'ils sont faisables de différentes façons,
et qu'il existe des manières de se simplifier la vie à leur égard.
Pas de feutre, pas de stylo plume, ça bave dès qu'il fait humide, et à la stupéfaction générale, ça arrive.
On écrit dans le livre de bord au stylo à bille, pour ne pas que ça s'efface.
On écrit sur les cartes au crayon à papier, il faut aussi une bonne gomme, qui n'efface que le crayon.
Il faut en général planquer ses crayons, il y a toujours un membre de l'équipage qui en a besoin, qui vous piquera le vôtre,
et qui oubliera de le remettre à sa place.
Il existe différents modèles de lampes de table à cartes, avec ou sans rhéostat, avec ou sans filtre rouge, sensé diminuer l'éblouissement consécutif à l'exposition à la lumière blanche, la nuit. Je n'ai encore jamais eu l'occasion de constater que ce genre de dispositif avait une influence quelconque sur ma vision,... mais ces filtres présentent cependant l'avantage de moins éblouir ceux qui essaieraient de dormir à proximité de la table à cartes.
Les lampes que je préfère pour l'heure sont les lampes frontales, en général disponibles dans la section "camping" de votre magasin de jouets favori. Elles sont également très efficaces dehors, où elles permettent de se passer des projecteurs de pont qui ont ce déplorable effet collatéral de mettre les batteries à plat en moins de temps qu'il n'en faut à un bègue pour réciter le Code Civil. Ce qui nous concerne d'autant plus que - je le rappelle - l'objectif est ici de naviguer sans électricité.
Les piles de la lampe frontale constituent une source d'électricité. Si on tient absolument à naviguer sans électricité, ce qui - ne le dites à personne - tutoie l'intégrisme, on n'aura qu'à se démerder avec une lampe à pétrole, et tant pis pour celui qui dort.
À ce sujet, le petit fanal, conçu pour être spécialement faible, destiné à éclairer la rose du compas de route sans éblouir le barreur, s'appelait le falot. Ce qui a donné lieu à ce qu'on appelle une "lumière falote"...L'estime se tient à l'aide du livre de bord, et de la (ou des) carte(s).
Dans le livre de bord, on consigne à intervalles réguliers, et à chaque fois que c'est nécessaire, l'heure et la date, le cap du bateau, et la valeur du loch (à défaut, la vitesse du bateau). Avec ces éléments, on est capable - ne serait-ce que graphiquement - de retracer le parcours du bateau ; et moyennant le fait qu'on sait d'où on est parti - ce qui est en général le cas, on peut savoir où on est.
La phrase qui précède est un résumé de la réalité. En effet, le cap du bateau ne suffit pas. Ce qu'il importe de connaître est en fait la Route Fond (Rf), celle qu'on suit sur la carte.
Le but premier du livre de bord est simple : il est là pour tenir l'estime.
En supplément, il permet de noter des phénomènes météorologiques susceptibles d'interférer avec la conduite du navire
(le baromètre s'est pris une baffe de 10 mb durant la dernière heure, le ciel bleu est devenu un tapis de stratus, le vent vire à l'ouest,
une houle d'ouest persiste et augmente, etc...).
Encore une fois, moyennant le fait qu'on sait à quoi sert un livre de bord, un simple cahier fait parfaitement l'affaire, à
l'inverse de ces publications qui y casent des rubriques comme "Achats à effectuer à la prochaine escale", dont l'aspect indispensable à la
tenue de l'estime peut ne pas paraître évident à tout le monde.
Ce qu'on écrit dans le livre de bord n'est pas ce qu'on griffonne sur un post-it. Il convient dans ce cas de rédiger plusieurs documents distincts.
Il y a à peu près autant de manières de tenir le livre de bord que de navigateurs...
C'est un domaine où peuvent s'exprimer des convictions d'un ordre quasiment religieux, parfois difficiles à faire remettre en question !
Je note en général dans le livre de bord les données suivantes :
Le loch, c'est quand on a un loch enregistreur. Sinon, on notera la vitesse.
Les données qui suivent servent à anticiper les changements de temps.
Vent (force et direction), Mer (état de la mer : calme, belle, peu agitée, agitée, grosse, forte, énorme...) Visibilité (analogue à l'humidité relative),
Baromètre, Nuages (en octas, et genre : 1/8 Cu - un huitième de cumulus, 2/8 CiSt - deux huitièmes de Cirro-Stratus, 8/8 St - il fait pas beau, etc).
En fonction de la zone ou on navigue, certaines données peuvent ne pas être aussi pertinentes qu'ailleurs. Par exemple, dans des zones tropicales, visi, baro et nuages s'avèrent ne pas être aussi utiles et indispensables qu'en Bretagne...
On note que la position du bateau ne fait pas nécessairement partie des données consignées dans les colonnes du livre de bord. C'est le genre de données qui sont obligatoirement portées sur la carte, laquelle doit être mise à jour en parallèle avec le livre de bord. Le fait de noter la position dans le livre de bord ne nuit certainement pas, mais c'est redondant.
En regard de la page de gauche, décrite ci-dessus, où sont notées ces données, je laisse une page blanche (à droite), disponible pour toute note complémentaire, ou qui peut apporter quoi que ce soit à la tenue de l'estime (...comme les heures de marée, la position du bateau, tiens donc ! ).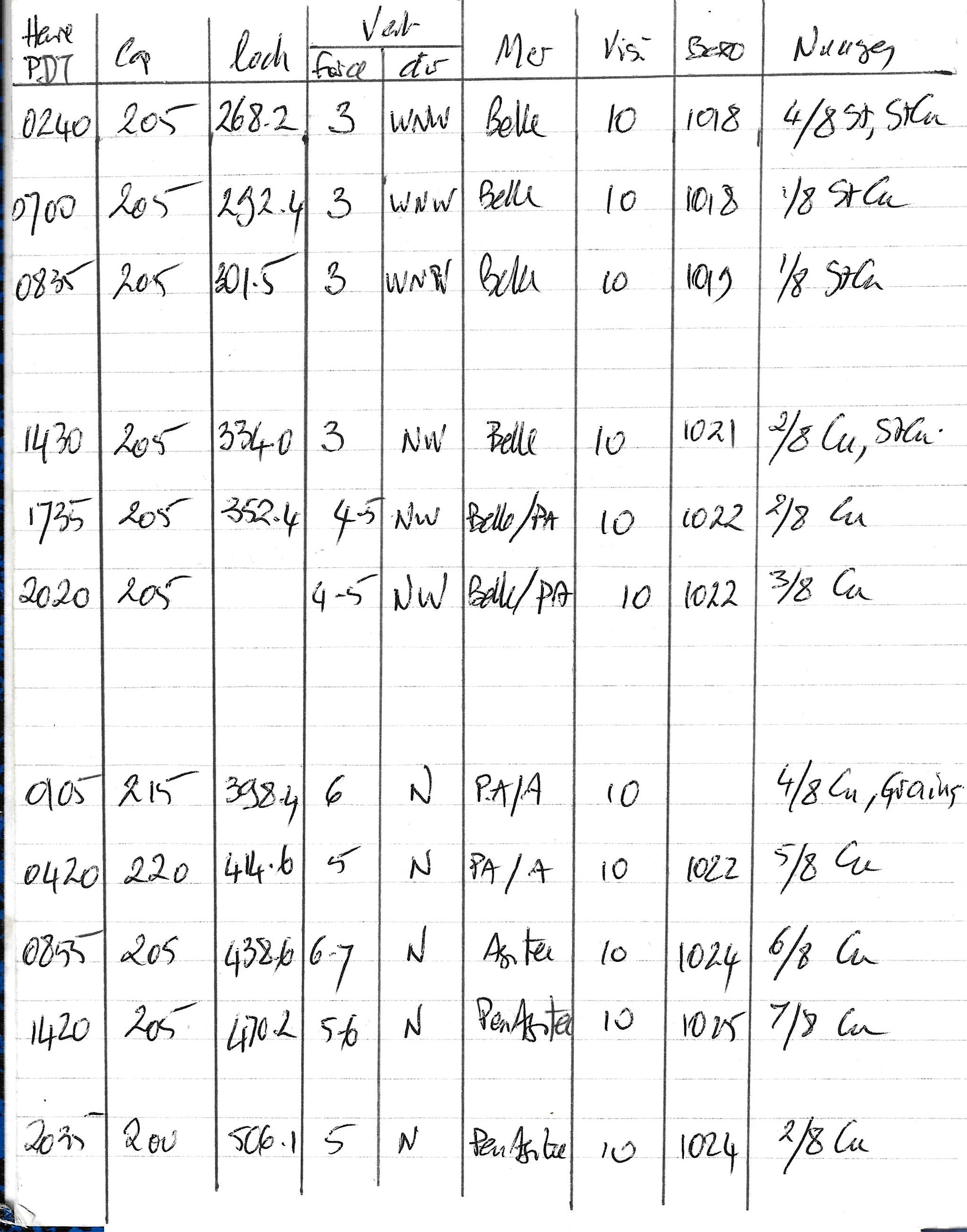
La déviation est une grandeur corrélée au bateau. Elle dépend des masses magnétiques (On dit bien magnétique, et pas métallique. Magnétique, c'est ce qui fait réagir un aimant. L'aluminium - par exemple - est métallique, il n'est pas magnétique) présentes à bord, et qui interagissent avec le compas. Il faut une courbe de déviation par compas. Si on a deux compas, il faut avoir deux courbes.
Sur un bateau en plastique ou en bois, la déviation est souvent de l'ordre de quelques degrés, d'un bord ou de l'autre. Un haut-parleur peut cependant lui faire faire des bonds de plusieurs dizaines de degrés. Sans blague.
Un bateau en acier - ou pire encore, en ferro-ciment - peut donner lieu à des déviations qui vont jusqu'à 50 degrés, d'un bord et de l'autre. C'est une grandeur à ne pas négliger.
On peut considérer que les courbes de déviation ont une équation générique de la forme suivante:
$$
d = a + (b \times \cos R) + (c \times \cos R) + (d \times \sin 2R) + (e \times \cos 2R)
$$
où d représente la déviation pour R, qui est le cap compas.
Si on peut enregistrer les données émises par une station NMEA (dans un endroit abrité, sans courant et sans dérive,
mesurer la différence entre HDG ou HDM et COG. RMC donne la déclinaison magnétique, en général) à l'aide d'un ordinateur
(ou d'un accessoire dédié), il est très facile d'obtenir les coefficients a, b, c, d et e par la méthode des moindres carrés.
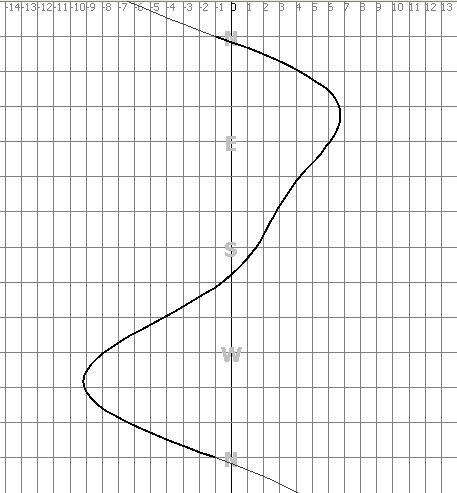
Une fois le Cap Compas (Cc) corrigé de la déviation, on obtient le Cap Magnétique (Cm).
La déclinaison magnétique est une grandeur propre à un lieu, à une date donnée. Elle est donnée par les cartes marines.
En Bretagne, elle est en ce moment (A.D. 2009) de l'ordre de 3°W. Vers Terre-Neuve, elle peut atteindre 40°W.
À San Francisco, elle est de 15°E.
Elle aussi, est à ne pas négliger. Si on part de San Francisco avec la Déclinaison de Terre-Neuve, on n'est pas forcément sûr du patois à utiliser à l'arrivée. Ça peut froisser des douaniers susceptibles...
Une fois le Cap Magnétique (Cm) corrigé de la Déclinaison, on obtient le Cap Vrai (Cv).
La dérive est engendrée par les conditions extérieures, le vent, les vagues (voire par le barreur, qui fait son boulot comme un cochon - c'est loin d'être exceptionnel). Un petit voilier y sera bien évidemment plus sensible qu'un super-tanker. Au près dans de la mer, une dérive de l'ordre de 10 degrés n'est pas exceptionnelle. La dérive est positive lorsqu'elle porte à tribord, négative lorsqu'elle porte à bâbord.
On peut supposer (rien de gravé dans le marbre) que la dérive puisse s'exprimer
$$
derive = derivemax \times \cos(AWA)
$$
où derivemax est de l'ordre de 10 degrés (c'est un paramètre propre au bateau), pour des angles de vent apparent (Apparent Wind Angle) entre -90° et +90°
Une fois le Cap Vrai (Cv) corrigé de la dérive, on obtient la Route Surface (Rs).
Le courant peut avoir plusieurs origines.
Le vent, la marée, des courants océaniques. Ces trois-là sont combinables à merci.
Les courants de marée sont donnés dans des tables et les atlas.
Les courants océaniques - comme le Gulf Stream - ont leur vitesse et direction données par certaines cartes (comme les Pilot Charts),
et d'autres documents (Instructions Nautiques, Coast Pilots, etc).
Le courant généré par le vent est déterminé par le pifomètre du navigateur !
Lequel peut être avantageusement assisté par l'estime tenue dans les heures précédentes.
Une fois la Route Surface (Rs) corrigée du courant, on obtient la Route Fond (Rf).
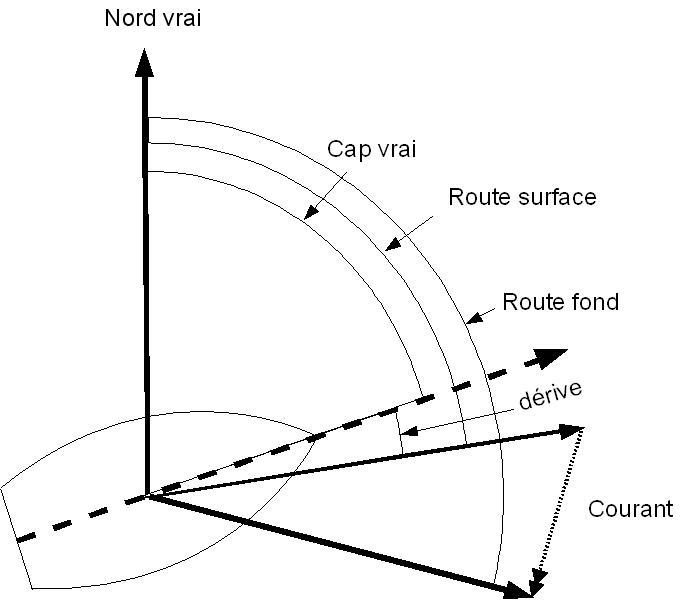
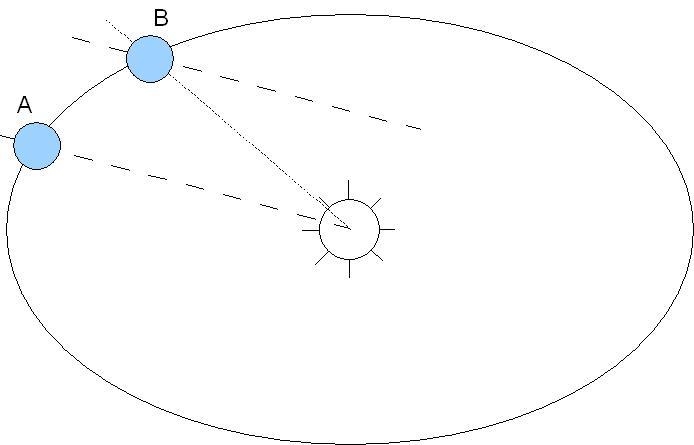
La figure précédente illustre les relations entre Cap Vrai (Cv), Route Surface (Rs) et Route Fond (Rf).
On y voit que la dérive est un angle, qui s'ajoute au Cap Vrai pour obtenir la Route Surface.
Tandis que le courant est un vecteur (caractérisé par une vitesse et une direction), qui s'ajoute (somme vectorielle) au vecteur Route Surface,
caractérisé lui aussi par une vitesse et une direction. En général, on se contente largement d'une résolution
graphique - effectuée sur la carte - pour cette somme de vecteurs.
L'opération qui consiste à partir du cap compas pour en déduire la route fond s'appelle "Corriger un cap".
L'opération inverse, qui consiste à donner au barreur le cap à suivre pour maintenir une route donnée s'appelle "Faire valoir la route".
Pour résumer:
On dispose du Cap Compas. On veut la Route Fond.
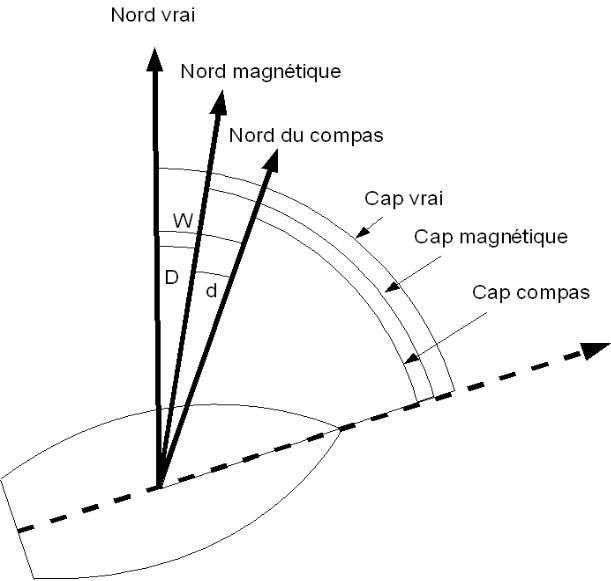
On obtient le Cap Vrai en ajoutant la variation (W) au Cap Compas (Cc).
La variation (W) est la somme algébrique de la déclinaison (D) et de la déviation (d).
La Route Surface (Rs) est la somme algébrique du Cap Vrai (Cv) et de la dérive.
La Route Fond (Rf) est la somme (vectorielle) du vecteur Route Surface (Rs) et du vecteur courant.
Pour recaler l'estime, on fait le point. En fonction de l'endroit où on est, des informations dont on dispose, les techniques de points sont différentes.
S'effectue en vue des côtes - on relève des amers, à l'aide d'un compas de relèvement.
Il est bon de disposer d'au moins trois amers, idéalement espacés l'un de l'autre d'environ 120 degrés...
On relève les amers au compas, on corrige ce relèvement compas pour en déduire le relèvement vrai, qu'on porte sur la carte.
Si l'observateur a fait un bon travail, on obtient à l'intersection des relèvements un (tout) petit triangle, qui contient la position du bateau.
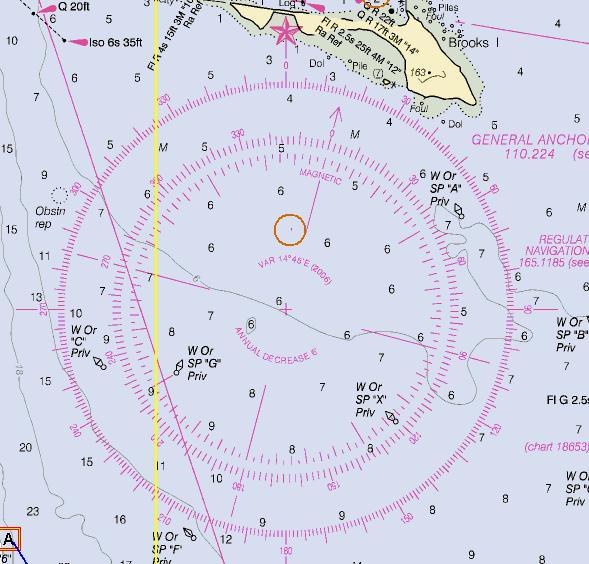
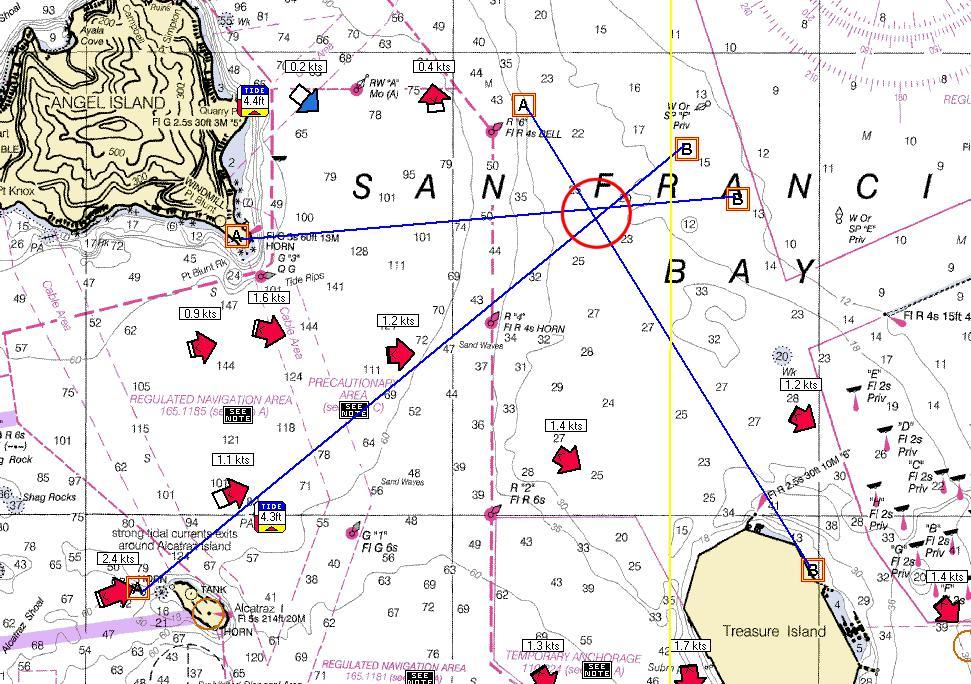
On estime d'abord la Déclinaison magnétique :
On voit sur la carte (voir la figure) que la Déclinaison était de 14°45' E en 2006, et qu'elle diminue de 6' par an.
En 2009 (année de référence pour ces calculs), elle a donc diminué de 18', ce qui la ramène à 14°27'E, qu'on arrondira à 14°E (D=+14).
Note à l'intention de ceux qui portent des lunettes :
On tenait auparavant les compas de relèvement à bout de bras. Depuis l'apparition du Mini-Morin (années 1970), les compas
de relèvement récents se tiennent près du visage. Si on porte des lunettes, et si ces lunettes se trouvent ne pas être
faites dans un matériau amagnétique, ceci peut générer des surprises.
Il existe une espèce particulière de relèvements, qu'on appelle des alignements.
Un alignement s'obtient lorsqu'on voit un amer par un autre. Comme "Le clocher par la balise", "la pointe par le château d'eau", etc.
L'alignement présente sur le relèvement deux avantages incontestables et énormes :
C'est la technique qu'on utilisera lorsque les trois amers nécessaires pour le point évoqué dans la section précédente ne sont pas disponibles.
S'effectue en vue des côtes, et fait intervenir le compas de relèvements, la route suivie (route fond), et distance parcourue. Il faut un loch fiable.
Si on ne dispose que d'un amer, on est fait un relèvement, qu'on porte sur la carte (relèvement vrai bien sûr). On note soigneusement le cap et la valeur du loch.
Plus tard, on effectue un nouveau relèvement du même amer, en même temps qu'on note la nouvelle valeur du loch. On porte le nouveau relèvement sur la carte.
On évalue ensuite la distance parcourue entre les deux relèvements, ainsi que la route fond suivie pendant ce temps.
Si nécessaire, on corrige cette donnée, en fonction du courant potentiellement subi.
À l'aide de la règle de Cras et du compas à pointes sèches, on case cette distance, sur cette route, entre les deux relèvements.
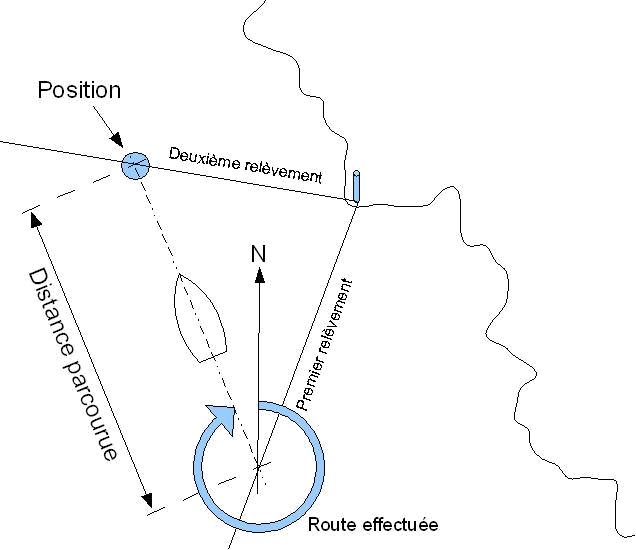
Faut vraiment être perdu..., cette technique n'est pas précise. Mais elle peut néanmoins servir à confirmer ou recaler une estime,
ce qui est toujours bienvenu.
Cette méthode est particulièrement bienvenue lors d'un atterrissage, après une traversée.
La remontée du fond va permettre de savoir à quel moment on aborde le plateau continental.
Si la sonde est une sonde à main, il faut avoir quelqu'un de dédié à cette fonction ; si on sonde des fonds de plus de 20 mètres,
c'est un travail à plein temps !
Néanmoins, cette méthode de point était couramment employée lors des atterrissages.
En effet, la navigation astronomique n'ayant pas toujours la précision requise pour enchaîner la navigation au large et la
navigation côtière - plus exigeante, précise et difficile, contrairement à ce que croient beaucoup de gens - le point par lignes de sonde - ou
au moins une vigilance renforcée à l'égard des sondes - permettaient de recaler l'estime élaborée à l'aide des méthodes de navigation astronomique.
Quand bien même sa précision pourrait faire l'objet de certains reproches, dans un contexte adapté, cette méthode prend tout son sens.
Le plus précis de tous, et de fort loin !
Il s'effectue en vue des côtes, et fait intervenir un sextant tenu horizontalement.
Voir à ce sujet l'appendice Arcs capables.
En plus d'être le plus précis, il est aussi facile à mettre en œuvre.
Voici pourquoi ce point est plus précis que le point par relèvements :
Lorsqu'on fait un point par relèvements, il faut stabiliser la rose du compas, ce qui constitue la principale difficulté de cette technique.
Lorsqu'on fait un point par arcs capables, on utilise le sextant tenu horizontalement.
Le sextant s'utilise en navigation astronomique pour abaisser un astre sur l'horizon, en d'autres termes, pour obtenir
l'angle que fait un astre avec l'horizon. En tenant le sextant horizontalement, on mesure l'angle que fait un amer avec un autre.
Il s'agit dans ce cas de mesurer l'angle entre deux amers - avec le sextant tenu horizontalement - et de tracer
ensuite sur la carte le cercle dont tous les points voient ces deux amers sous le même angle.
Voici comment on procède :
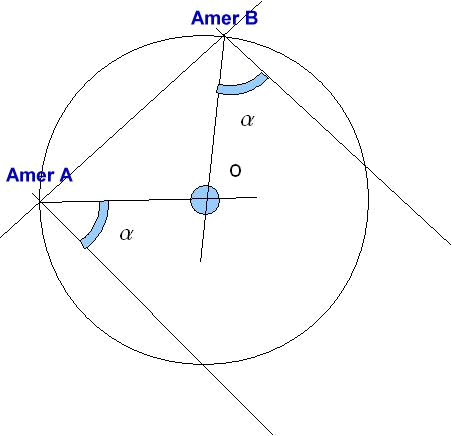
Voici ce qu'on obtient avec 3 amers, on est à l'intersection des deux cercles :
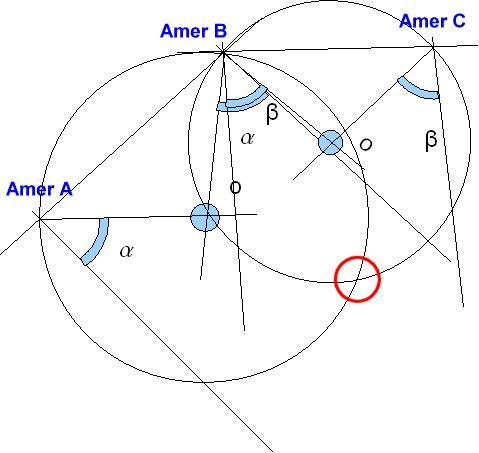
Traité en détails dans une prochaine section. C'est de toute évidence la technique qui demande le plus de calculs.
Comme on le verra dans la section qui lui est consacrée, certains aspects de la navigation astronomique requièrent la connaissance du temps, aussi précisément que possible. Il existe des techniques qui permettent de recaler les chronomètres, à partir de l'observation de la distance (angulaire) qui sépare la Lune des autres astres (Soleil, planètes, étoiles). Cette technique met en œuvre encore plus de calculs que le point astronomique proprement dit. Mais ça fonctionne. Les tables qui permettent de connaître cette distance lunaire ont cessé d'être publiées en 1907 (date à laquelle des tops horaires ont commencé à être émis par radio), mais grâce à l'informatique, on est en mesure de re-publier ces tables.
La connaissance de l'état de la marée permet de savoir deux choses importantes :
À la main, on utilisera la règle des douzièmes. Elle permet une approximation tout à fait satisfaisante de la sinusoïde que suit en fait la hauteur d'eau.
Attention !! Tous les pays (éditeurs des cartes et des almanachs) n'utilisent pas la même référence pour le zéro des cartes !
Dans l'ordre des priorités, immédiatement après avoir identifié le zéro des cartes, il convient aussi d'identifier l'unité utilisée. On trouvera des cartes graduées en mètres, en pieds, et en brasses. Une brasse équivaut à six pieds (et une encablure à 100 brasses), le mètre à un peu plus de trois ; avoir une idée de son tirant d'eau dans chacune de ces trois unités peut sans doute contribuer à une certaine forme de sérénité, si on doit avoir recours à des cartes établies de ces différentes façons... Avec trois brasses d'eau, on n'a pas pied. Avec trois pieds, si, et largement.
Sur les cartes normales, les sondes et les altitudes sont exprimées en mètres. Sur d'autres cartes, il n'est pas exceptionnel d'avoir les sondes en brasses, et les altitudes en pieds. On ne rit pas.
La marée est décrite par la superposition de plusieurs courbes sinusoïdales, en général au nombre de neuf (mais ça peut aller jusqu'à 92).
Les coefficients à appliquer à chacune de ces courbes sont appelés les coefficients harmoniques, qui varient en fonction du temps,
et de l'endroit. La détermination de ces coefficients harmoniques est la clé de l'élaboration des tables et almanachs de marée.
La différence de hauteur entre la marée haute et la marée basse est appelée l'"amplitude", la différence de temps
qui sépare l'heure de la marée haute et l'heure de la marée basse est appelée la "durée".
Il existe plusieurs sortes de marée, de semi-diurne à diurne, en passant par les marées à inégalités diurnes...
Néanmoins, lorsqu'il s'agit de calculer la hauteur d'eau, la règle des douzièmes demeure une valeur sûre.
D'autant que - répétons-le - la hauteur d'eau n'est malheureusement pas déterminée par les seuls coefficients harmoniques.
La pression atmosphérique, le sens et la force du vent ont une influence considérable sur la marée, qui ne saurait malheureusement être
prise en compte lors du calcul des almanachs. Les outils dont on dispose à bord pour évaluer cette influence sont pour
l'heure de nature pifométrique ou assimilée.
[1, 2, 3, 3, 2, 1], et 1+2+3+3+2+1 = 12
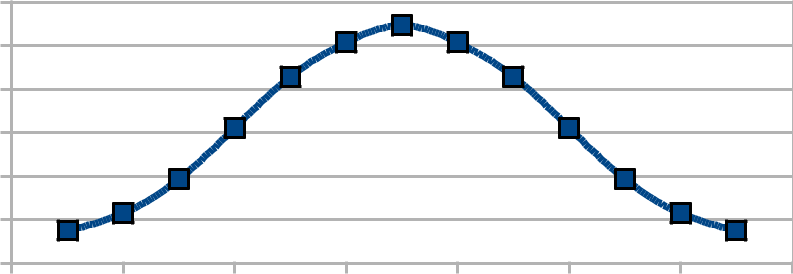
Voilà un vaste sujet. Les prévisions qu'on sera capable de produire sans électricité vont être basées sur
l'observation, et pas sur la réception de documents (bulletins, fax, GRIBs).
Le livre de bord contribue pour une bonne part à prendre note de ces observations.
Vitesse et direction du vent, associées à la pression atmosphérique lue au
baromètre seront les données mesurées, la nébulosité (nuages en octas et genre,
associés à la visibilité) sera observée. La valeur de la pression lue au baromètre n'est pas aussi
importante que la variation dont elle fait l'objet. Le fait que la pression affichée soit de 1010 ou de 1030 n'est guère important.
Le fait que cette pression augmente ou diminue de 15 millibars en heure va avoir une importance majeure.
L'évolution de la forme des nuages, de la visibilité, de la pression atmosphérique, de la direction et de la force du vent
sont autant de paramètres qui vont permettre d'anticiper l'approche ou l'évolution d'une perturbation.
Comme tels, ils seront soigneusement consignés dans le livre de bord.
La façon d'interpréter ces paramètres dépasse de beaucoup le cadre de ce document.
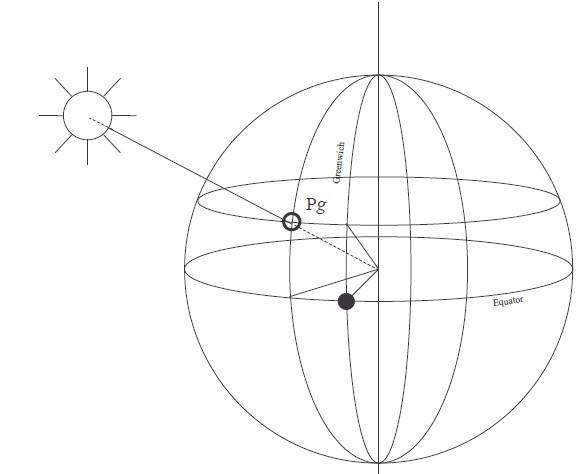
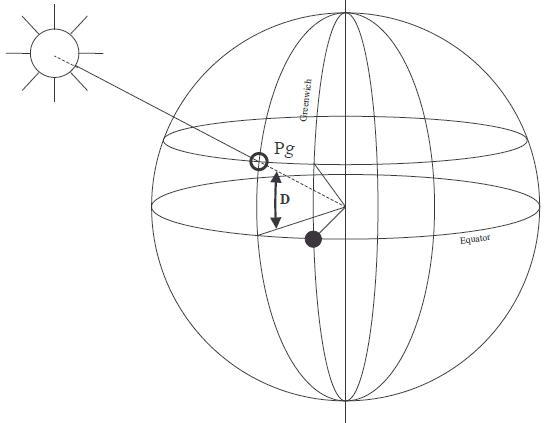
Les calculs sont simples. Il va s'agir de quelques additions, et de quelques interpolations.
Point n'est besoin de tables trigonométriques ou logarithmiques. Papier et crayon suffisent.
Le point par hauteur méridienne exploite un cas particulier, qui est celui où l'astre et l'observateur sont sur le même méridien.
Il est midi au lieu de l'observateur (si tant est que l'astre observé soit le Soleil).
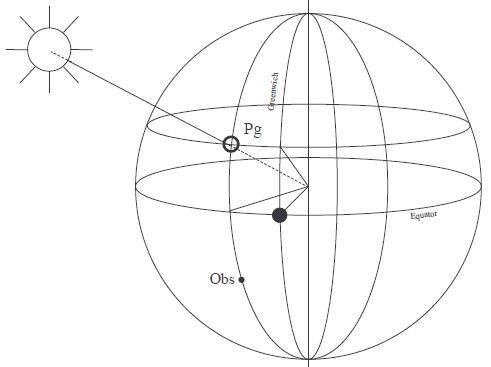
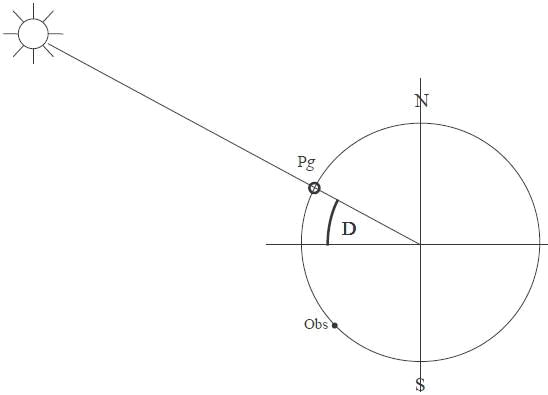
On introduit ici une nouvelle notion, celle de distance zénithale, notée Dz, ou ζ (lettre grecque dzeta).
La distance zénithale est le complément de la hauteur, soit (90˚ - hauteur).
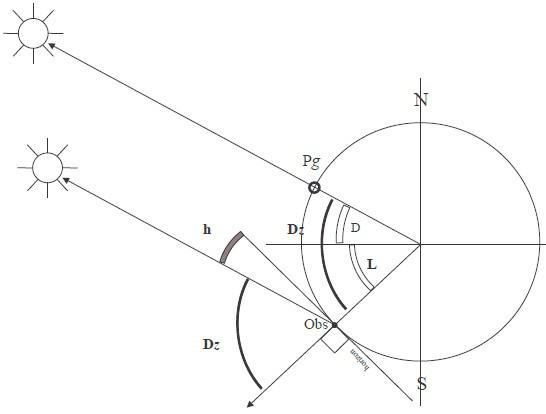
C'est à la fois très simple, et un peu compliqué. La théorie est très simple, la pratique est - à la surprise générale - plus scabreuse.
Le principe repose sur le fait que la terre tourne de 360° sur elle-même en 24 heures. Il existe donc une étroite corrélation entre la longitude et l'heure (il est possible que le terme "angle horaire" vous ait mis la puce à l'oreille). Si un astre passe à un méridien à une heure donnée, il passera exactement une heure plus tard à un méridien situé 15° plus à l'ouest.
Les éphémérides nous permettent de savoir à quelle heure le soleil culmine à Greenwich. Si on arrive à savoir à quelle heure le soleil culmine sur le méridien de l'observateur, alors il suffit d'exprimer cette différence de temps en différence d'angle pour connaître sa longitude.
Ceci requiert cependant un chronomètre précis. En effet, 360° en 24 heures signifie 15° en une heure. Soit 15' en une minute (de temps), ce qui représente 1' en quatre secondes (de temps). Ainsi donc, une erreur de 4 secondes sur la montre correspond à une erreur d'une minute de longitude. Comme on l'a déjà remarqué, ça va vite !
D'autre part, ainsi qu'on va le voir, l'heure exacte de la culmination n'est pas la donnée la plus facile à obtenir.
Une fois de plus, il faut disposer de sa position estimée, et de la date.
Il s'agit ici de mettre en œuvre la technique énoncée précédemment.
Pour cet exemple, on considère que l'astre observé est le soleil, mais ceci est valable pour tous les astres observables. Il est même possible pour d'autres astres que le soleil d'utiliser la hauteur anti-méridienne (au minuit de l'astre, et non pas à son midi, c'est-à-dire non pas lorsqu'il culmine, mais lorsqu'il atteint son point le plus bas).
Supposons qu'on soit le jeudi 8 octobre 2009, et que l'estime nous situe par 34°04' N et 127°54' W.
La première chose à savoir, c'est à quelle heure cette hauteur méridienne va se produire.
On va procéder ici à une série d'interpolations. On les fait ici à la main, afin d'en détailler le processus. Des tables de conversions destinées à cet usage sont fournies dans un document séparé, en annexe.
On va donc convertir sa longitude estimée de degrés en heures. Une heure représente 15 degrés (15° en 1 heure = 360° / 24 heures).
Ainsi, 127° = (127 / 15) = 8.466 heures, et 54' = (54/60) / 15 = 0.06 heure.
Donc 127°54' équivaut à 8.526 heures. 0.526 heures = (0.526 × 60) minutes, soit 31.56 minutes, soit encore 31 minutes et 33.6 secondes.
La longitude est ouest, ainsi il sera midi à notre longitude estimée 8 heures 31 minutes et 34 secondes (arrondi) plus tard qu'à Greenwich.
Attention: Contrairement à une rumeur couramment répandue, il n'est pas midi tous les jours à la même heure !
Ceux pour qui c'est nouveau consulteront avec profit et à ce sujet l'appendice Équation du temps.
Les éphémérides nautiques donnent l'équation du temps. L'équation du temps représente l'intervalle qui sépare 12:00 UT de l'heure de la culmination du soleil (qu'on appelle aussi "temps de passage au méridien").
Pour le 8 octobre 2009 (voir les éphémérides de cette date, plus avant dans le document), l'équation du temps à midi UT est de +12m 29s. On doit effectuer une interpolation. Une interpolation linéaire est suffisante ici. Le lendemain, 9 octobre 2009, l'équation du temps à midi UT est de +12m 46s, elle augmente donc de 17s en 24 heures. Notre longitude représente comme on l'a déjà calculé 8.526 heures, on doit donc ajouter à l'équation du temps la valeur suivante en secondes (17 / 24) × 8.526, soit 6.06 secondes. L'équation du temps à l'heure du passage du soleil à notre longitude estimée est donc de +12m 35s.
Attention, ceci signifie que la culmination (passage au méridien) du soleil à notre longitude estimée se produira 12m 35s avant le midi légal. Soit 8h 31m 34s - 12m 35s, à savoir 20h 18m 59s UT.
Les éphémérides donnent aussi le temps de passage des astres au méridien de Greenwich. On peut aussi procéder à la même interpolation à partir du temps de passage. Équation du temps et temps de passage sont en effet des données redondantes. Dans notre exemple, le temps de passage du soleil à Greenwich le 8 octobre est 11:47:30.113 UT, et le 9 octobre 11:47:13.572 UT. Chacun choisira la méthode qui lui convient le mieux.
On trouverait ainsi un temps de passage à notre méridien estimé de 11:47:24 UT.
11h 47m 24s + 8h 31m 34s = 20h 18m 58s UT. C'est pareil.
On peut également anticiper la hauteur qu'on devrait observer si l'estime était correcte.
À 20 heures UT le 8 octobre 2009, la déclinaison du soleil est S 6°10.09', à 21 heures, elle est S 6°11.04'.
Elle augmente donc de 0.95' en une heure. On peut ici interpoler de tête, on arrondi 18m 59s à 20 minutes, soit 1/3 d'heure.
0.95' / 3 = 0.3166'. La déclinaison du soleil à l'heure estimée de la culmination sera donc de S 6°10.406', qu'on arrondira à S 6°10.40'.
Latitude et déclinaison sont de signes différents, donc Dz = L + D, à savoir 34°04' + 6°10.4' = 40°14.4'. Ainsi, la hauteur observée (théoriquement) devient 90° - 40°14.4', soit 49°45.6'.
Reste à savoir si c'est vrai ! On sort le sextant, et on commence à observer.
On commence à observer suffisamment longtemps avant l'heure estimée de la culmination, pour être sûr de ne pas la manquer.
Cet intervalle de temps dépend de la qualité de l'estime.
On continue ainsi à observer l'astre tant que sa hauteur augmente.
Dès lors que l'astre commence à redescendre (que l'astre commence à se mouiller - Le sextant permet par son jeu de miroirs de
descendre l'astre sur l'horizon. On dit qu'on "mouille" un astre lorsqu'il trempe dans l'eau dans le miroir du sextant),
c'est qu'on a atteint la culmination, et qu'on dispose maintenant de la hauteur instrumentale.
Pour notre exemple, on a lu sur le sextant 49°32'.
C'est pas fini !
La hauteur instrumentale doit être corrigée, pour obtenir la hauteur observée.
Il faut lui apporter quatre - voire cinq - corrections:
On verra plus loin un exemple de la façon d'obtenir la valeur de ces correction, grâce à des tables de correction, dans la section consacrée aux droites de hauteur avec des tables de calcul.
Le semi-diamètre s'applique au soleil et à la lune, car on abaisse le bord inférieur de l'astre (parfois supérieur dans la cas de la lune si le bord inférieur n'est pas disponible, à cause de la phase de l'astre, ou si un nuage masque le bord inférieur) sur l'horizon, et non pas son centre.L = 40°15.4' - 6°10.4' = 34°05.0' N
C'est possible, à condition bien sûr de disposer d'un chronomètre fiable.
Ce qu'il faut, c'est avoir l'heure exacte de la culmination, l'ajouter ou la retrancher au temps de
passage (midi corrigé de l'équation du temps), de transformer cette grandeur en angle, comme on l'a fait
en sens inverse pour savoir à quelle heure commencer à observer, et le tour est joué !
Le problème, c'est qu'à cette heure, le soleil a une course dans le ciel qui tangente l'horizontale, et que le
moment où la culmination est effective est impossible à déterminer avec la précision requise ;
on rappelle que 4 secondes de temps représentent une minute de longitude, et que c'est justement la longitude qu'on cherche à déterminer...
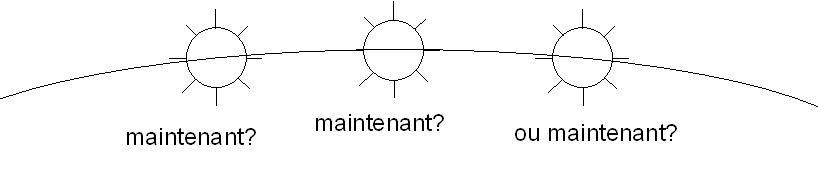
On fait une première observation environ 15 minutes avant l'heure estimée de la méridienne.
On note précisément à quelle heure T1 la hauteur a été prise. On appelle la hauteur "H1".
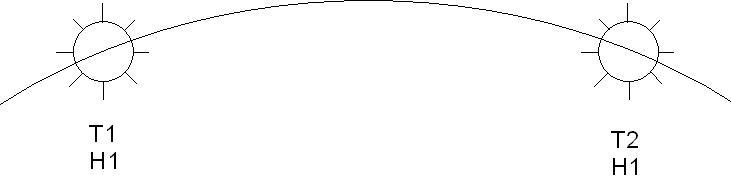
Exemple:
On a pris la première hauteur H1 à T1 = 20:05:00 UT.
Le soleil est repassé par la même hauteur H1 à T2 = 20:33:10 UT.
La moyenne de ces deux temps est 20:19:05 UT.
Le temps de passage à Greenwich a été calculé précédemment,
c'est 11:47:24 UT, ce qui constitue une différence de 8h 31m 41s.
8h = 8 × 15° = 120°
31m = (31 / 60) × 15° = 7,75°
41s = (41 / 3600) × 15° = 0,171°
On obtient donc un angle horaire de 120 + 7,75 + 0,171 = 127,921° soit une longitude de 127°55,26' W.
On est ainsi passé d'une position estimée de 34°04' N et 127°54' W à une position corrigée de 34°05.0' N et 127°55.26' W.
Un premier commentaire:
On remarque que lors de la recherche de la latitude, on n'a besoin de l'heure que pour savoir à quelle heure commencer l'observation ;
la précision de la minute (de temps) est fort suffisante.
Par contre, lors de la recherche de la longitude, la précision du chronomètre impacte directement - et considérablement - la
précision du calcul de la longitude. À nouveau, quatre secondes sur le chronomètre représentent une minute d'arc en longitude.
Un deuxième commentaire:
Il faut peu de temps de pratique du sextant pour réaliser qu'il est présomptueux de vouloir effectuer des mesures d'une
précision plus fine que la minute d'arc, surtout sur un petit bateau.
Les interpolations nécessaires pour le calcul des différentes valeurs issues des éphémérides peuvent en être facilitées.
Ainsi, pour le calcul de la déclinaison, on a trouvé une variation horaire de 0.95'. En pratique, on arrondira à 1', et tout ira bien.
Il n'y a guère de raisons de s'encombrer de dixièmes de minutes d'arc.
Attention cependant aux arrondis, il faut arrondir à la minute la plus proche, et ne pas se contenter de la partie entière.
Les calculs sont plus complexes, on va voir pourquoi.
Un des intérêts du point par droite de hauteur est qu'il n'est pas nécessaire d'être au midi vrai pour le faire,
contrairement à la méthode décrite ci-dessus.
Le principe du point par droites de hauteur repose sur les données suivantes :
On a vu dans la section consacrée au point par hauteur méridienne le rapport qu'il existe entre latitude, déclinaison, et distance zénithale. On va introduire ici la notion de "grand cercle".
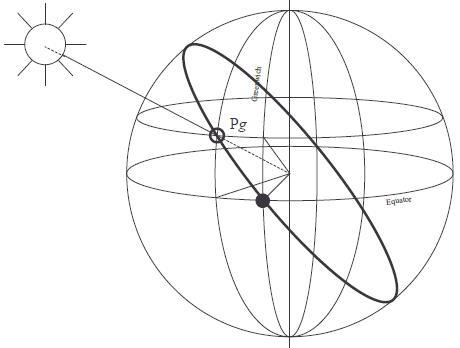
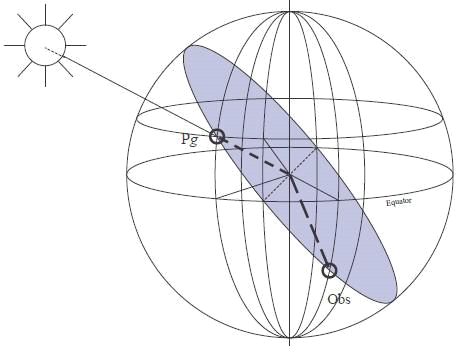
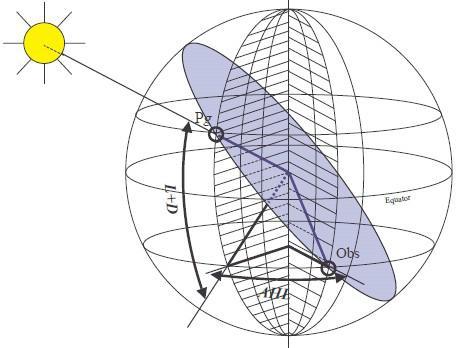
Encore une définition :
L'azimut, noté Z, est le relèvement vrai du point Pg, qui sera donc compté de 0° à 360°. En d'autres termes : "Dans quelle direction voit-on ce point Pg ?".
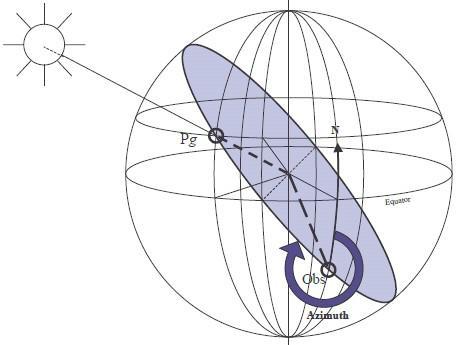
On veut calculer, pour la position estimée de l'observateur, à l'heure exacte de l'observation :
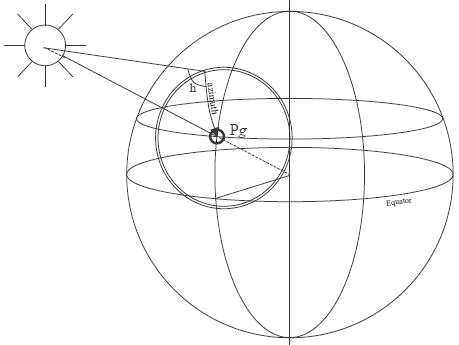
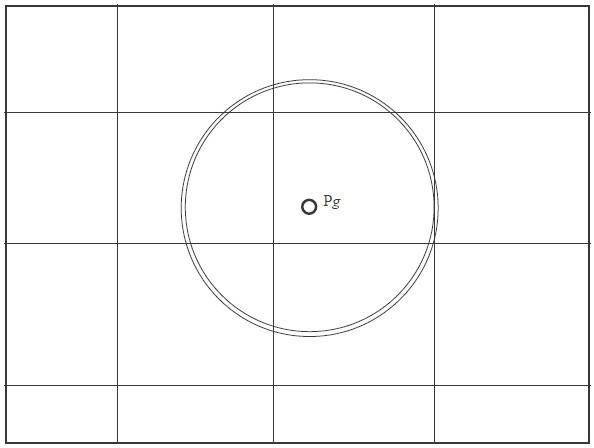
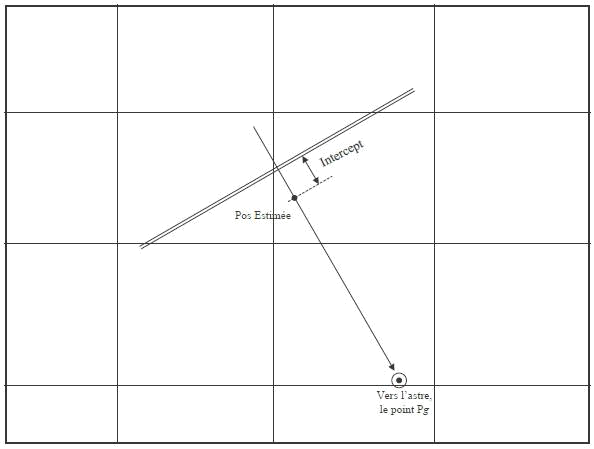
On le saura lorsqu'on disposera de l'intersection avec... une autre droite.
Si on dispose de plusieurs astres (si il fait nuit par exemple, la lune, les planètes, les étoiles...),
il suffit de faire plusieurs droites consécutives.
Sinon, on attend, et on en refait une sur le même astre. Son azimut ayant varié, on aura alors une intersection.
Il faut cependant translater la première droite, de la distance parcourue dans l'intervalle, dans la direction de la
route fond, ça s'appelle un "transfert de droite". Le point corrigé se situe à l'intersection des droites corrigées de l'intercept.
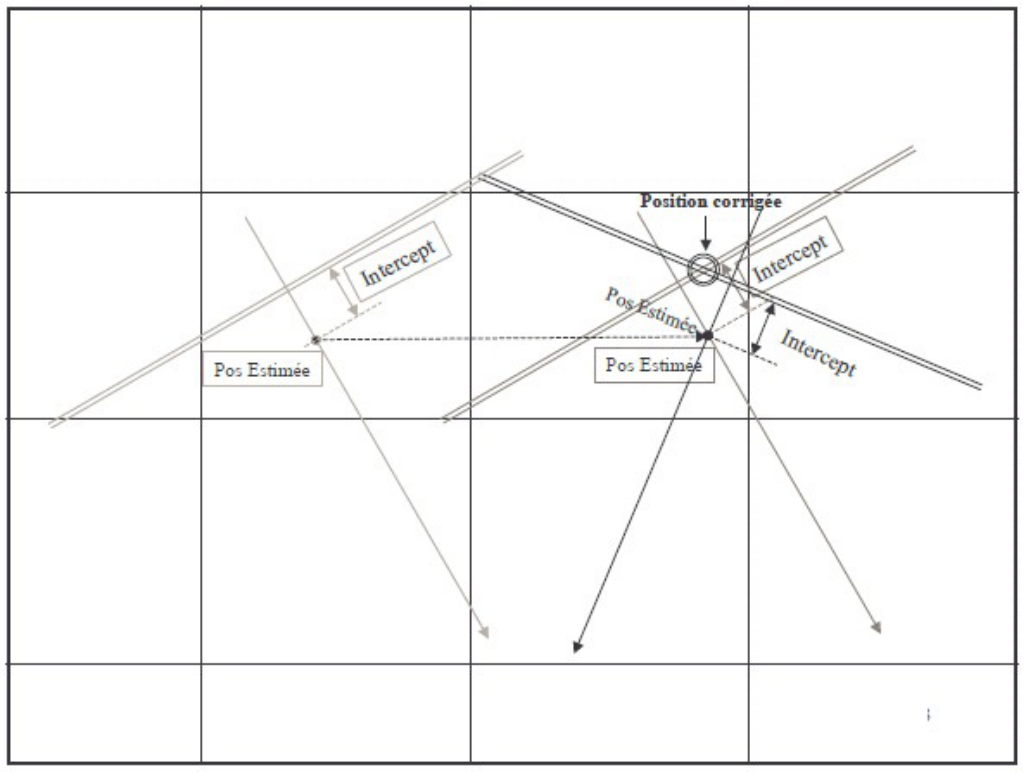
On peut aussi résoudre ce genre de figures de manière algébrique ou arithmétique. Mais pourquoi faire ? Au-delà du nombre d'étapes de calcul que cette résolution implique (il s'agit de trigonométrie sphérique), les éventuelles erreurs seront probablement plus évidentes dans le contexte de la résolution graphique. Et encore une fois, la précision du trait sur la carte est clairement supérieure à la précision de la mesure effectuée avec le sextant, voire avec le chronomètre. Il convient sans doute de garder cet ordre de grandeur en tête...
Note: Dans ce qui précède, on ne dispose que du Soleil. On est donc obligé d'attendre qu'il se déplace entre chaque observation - et donc droite de hauteur. Si on dispose de plusieurs astres - comme le Soleil et la Lune, ainsi que ça arrive - on peut effectuer des observations nettement plus rapprochées dans le temps. De nuit, ça peut être encore plus efficace, Lune, planètes, étoiles, peuvent être observables quasiment simultanément. La seule contrainte dans ce contexte nocturne est de disposer d'un horizon net.
On suppose pour l'exemple qu'on est le jeudi 8 octobre 2009, à 20 heures 47 minutes et 38 secondes UT,
et que l'estime nous situe par 37°46' N et 122°37' W.
On observe le soleil, et on a lu sur le sextant une hauteur (instrumentale donc) de 44°20'.
Qu'on procède avec des tables de logarithmes ou avec des tables plus élaborées, il va falloir obtenir les coordonnées du point Pg
de l'astre observé, à avoir le soleil.
Ces coordonnées du point Pg sont - on le rappelle - l'Angle Horaire à Greenwich et la Déclinaison.
Ceci s'obtient dans les éphémérides.
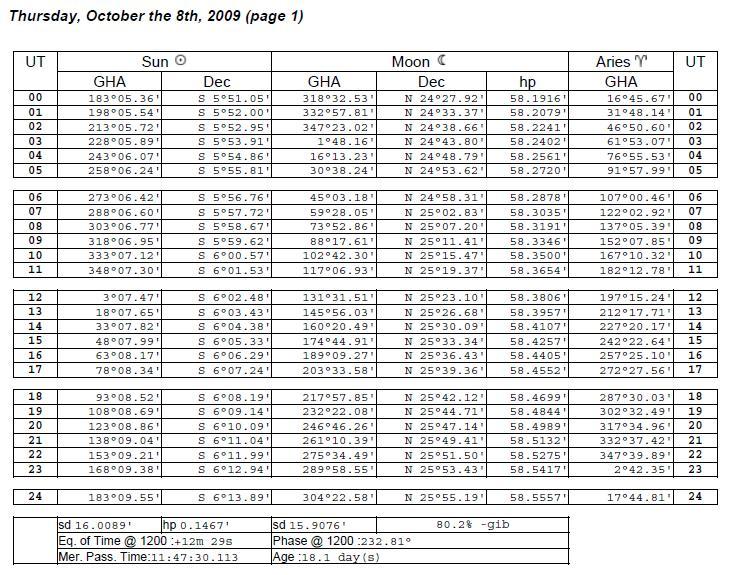
On trouve l'Angle Horaire à Greenwich dans les éphémérides, dans la colonne GHA (Greenwich Hour Angle) du Soleil.
À l'heure ronde inférieure, à savoir 20 heures, on lit AHG=123°08.86'.
Il est 47m 38s plus tard, quelle partie décimale d'une heure ceci représente-t-il ?
47m = 47 × 60 s = 2820 s.
47m 38s = 2820 s + 38 s = 2858 s.
En heures, ceci représente 2858 / 3600 = 0.793888 heure.
Entre 20 et 21 heures, l'AHG a varié de 123°08.86' à 138°09.04', soit une augmentation de 15°00.18' (là, on chipote.
On pourrait très bien se contenter de dire que l'Angle Horaire varie de 15° par heure).
On interpole cette variation, de façon linéaire, et on considère qu'en 47m 38s (0.793888 h),
l'AHG a augmenté de 15°00.18' × 0.793888 = 11°54,64'.
L'AHG à l'heure de l'observation sera donc 123°08.86' + 11°54.64' = 135°03.5'.
De même, on trouve la déclinaison du soleil à 20 heures dans les éphémérides, elle est S 6°10.09'.
À 21 heures, elle est de S 6°11.04', elle augmente donc de 0.95' en une heure.
En 47m 38s, elle aura donc augmenté de 0.95' × 0.793888 = 0.75419', ce qui la porte ainsi à S 6°10.84'.
On a donc maintenant les coordonnées de Pg:
AHG : 135°03.5'
D : S 6°10.84'
Reste à calculer l'Angle Horaire Local (AHL). La longitude est ouest, on la retranche de AHG:
AHL = 135°03.5' - 122°37' = 12°26.5'.
La dernière étape est de corriger la hauteur instrumentale, pour en faire une hauteur observée. La même table que celle qu'on a utilisé pour la hauteur méridienne donne une correction positive de (12.59' + 0.1'). Ce qui porte la hauteur observée à 44°32.69'.
On dispose maintenant de tous les éléments nécessaires pour entamer le calcul.
Compte tenu de la précision requise, l'usage des logarithmes est nécessaire.
Comme on va le voir ensuite, on peut
Les tables de navigation facilitent le calcul, en minimisant le nombre d'étapes, et par là même le nombre de sources d'erreur.
Avec les tables de Dieumegard, le calcul de la hauteur se réduit à 8 étapes, et avec les tables de Bataille,
le calcul de l'azimut est fait en 5 étapes.
Il est intéressant de constater que ces tables (Dieumegard et Bataille) ont été publiées au vingtième siècle, après 1930 (Jean-Baptiste Dieumegard était un capitaine au long cours né en 1910). Il a existé d'autres tables auparavant, mais il est également hautement probable que l'essentiel des calculs s'effectuaient avec des tables de logarithmes.
Pour ceux que la manipulation de ces tables intéresse, on fournit ici une page qui permet de valider ses résultats, étape par étape.
Voici comment ces tables fonctionnent. Elles parcourent le même chemin que le procédé décrit auparavant, celui qui ne met en œuvre que les table de logarithmes. Ces tables permettent de réaliser plus vite les mêmes opérations.
Les tables de Dieumegard se composent en fait de 4 tables : 1, 2, 3, A.
colog(1 - cos(a))colog(cos(a))colog(n)1 - cos(a)
Note : cologarithme, colog(x) = log(1/x)
Le recours aux cologarithmes permet de n'avoir (sauf exceptions, caractéristiques surlignées) à manipuler que des valeurs positives.
Voici d'abord un formulaire, qui guide l'utilisateur dans l'usage des tables de Dieumegard. Les étapes sont détaillées ensuite.
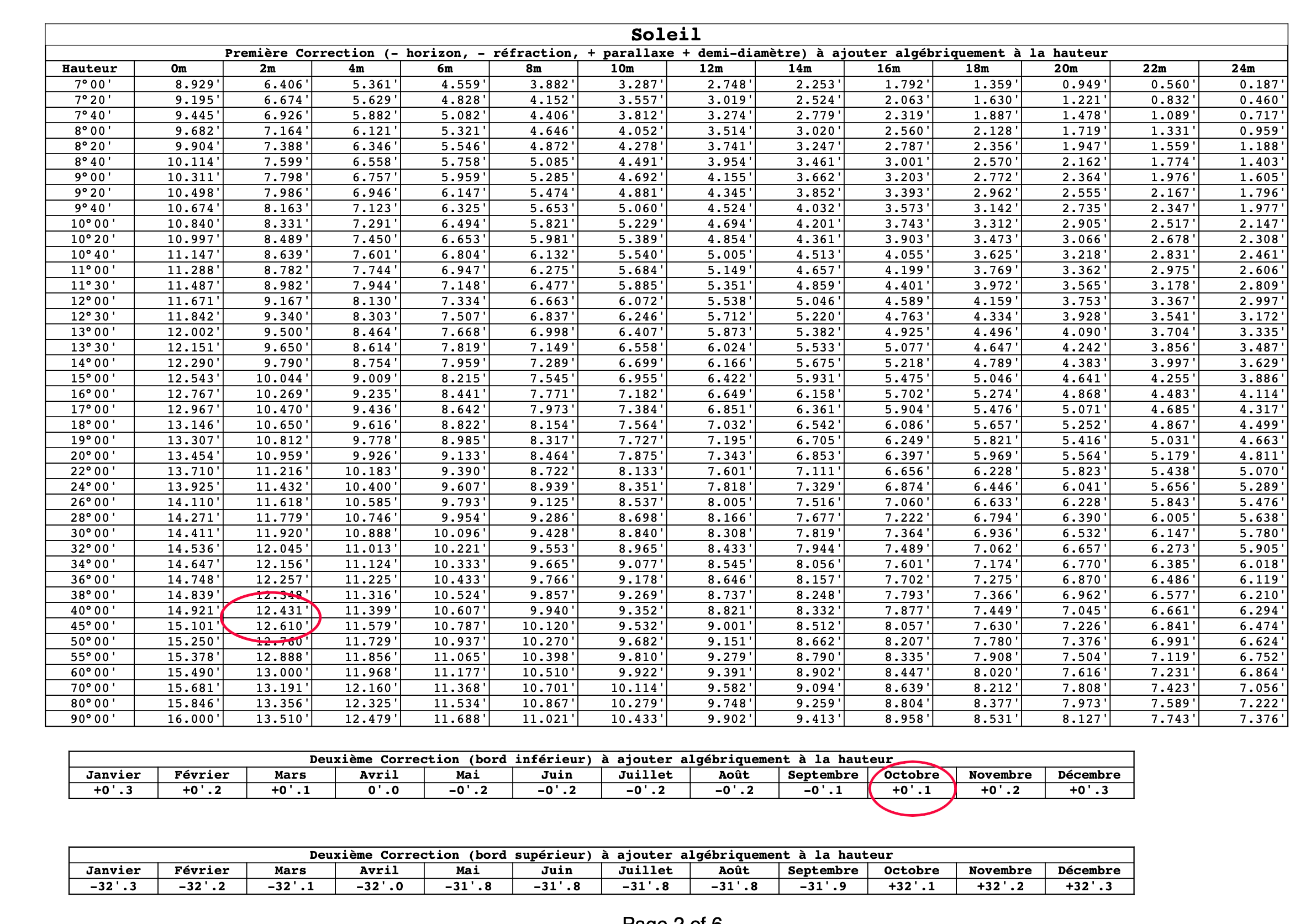
44°20', on arrondit
la première correction à + 12.59', et la deuxième est de +0.1'. Ce qui donne un total de + 12.69'.
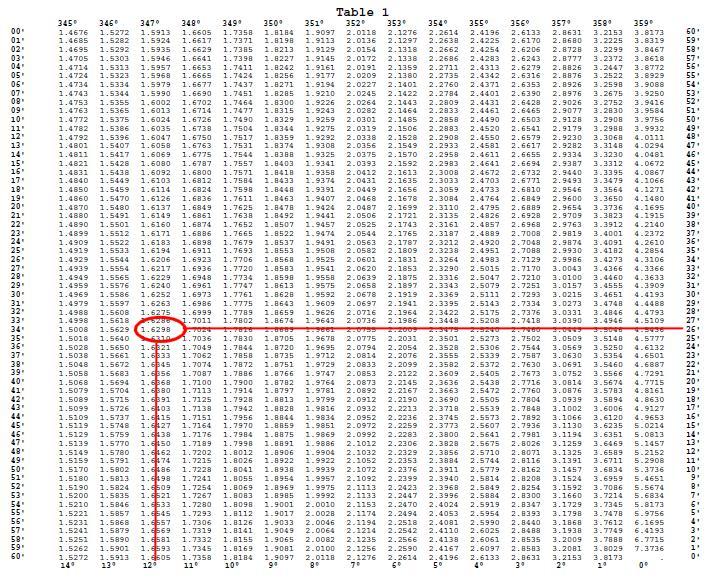
a = 1.6298
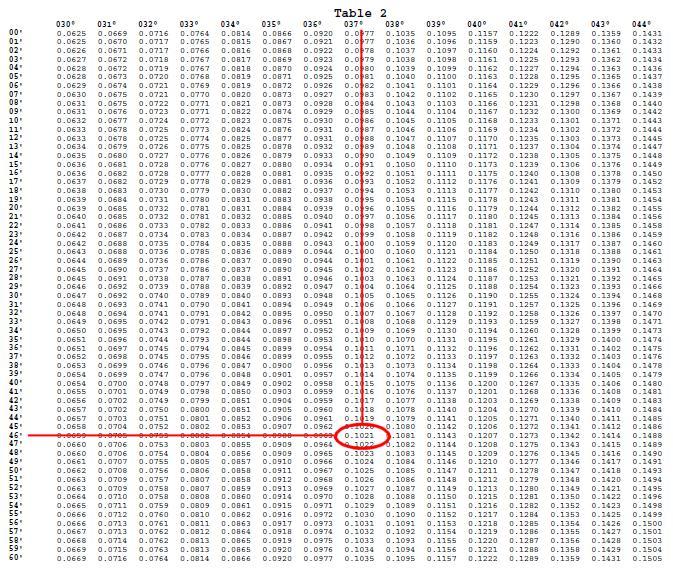
b = 0.1021
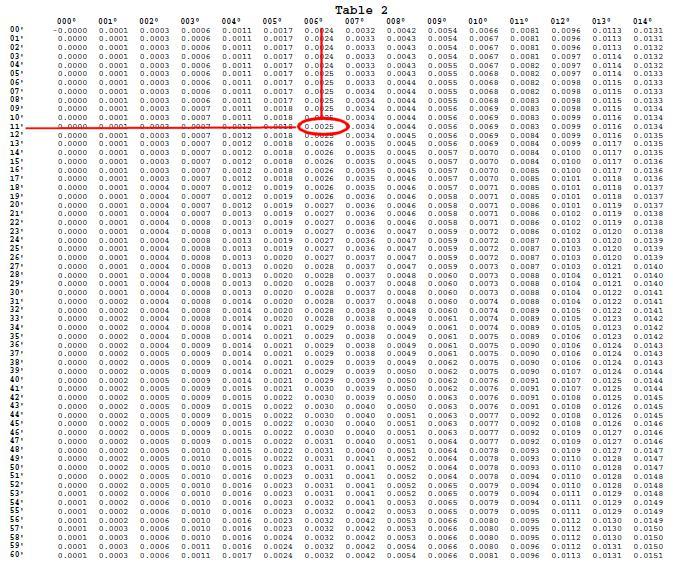
c = 0.0025
On calcule ensuite la somme d = a + b + c = 1.6298 + 0.1021 + 0.0025 = 1.7344
01 en haut, et entre 84 et 85 à gauche, qu'on pose 84.5, ce qui nous donne
e = 0.01845
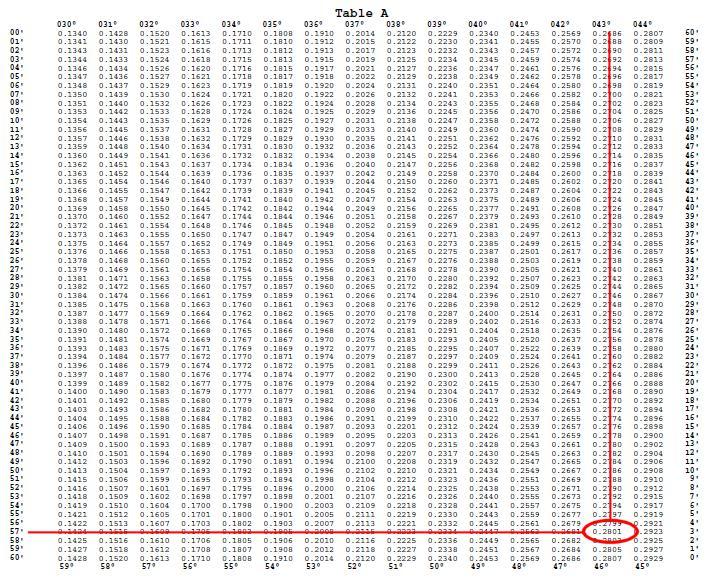
f = 0.2801
On calcule ensuite la somme g = e + f = 0.01845 + 0.2801 = 0.29855
44°33'
Comme pour les tables de Dieumegard, on va commencer par le formulaire, et détailler ensuite les différentes étapes :
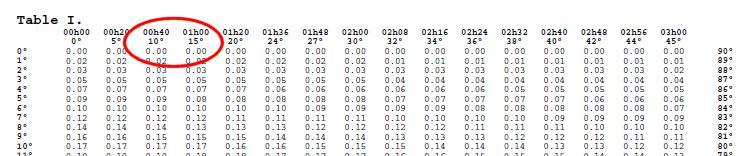
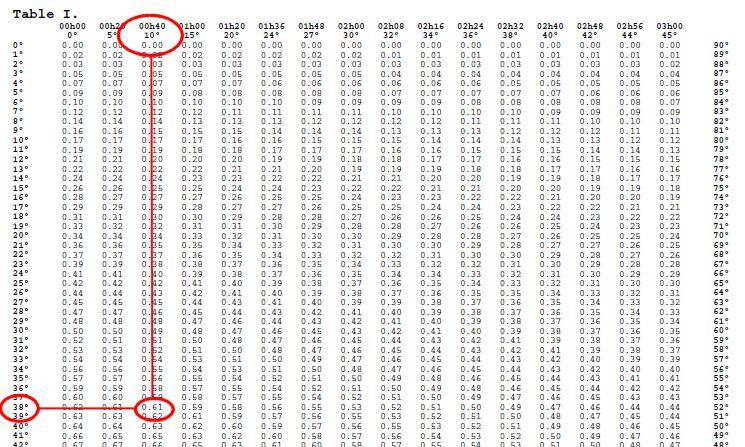
nombre m = -0.61.
nombre n = -0,08.
m+n, -0,61 et -0,08) est égale à -0.69, qu'on cherche à l'intérieur de la table II, avec l'angle au pôle à droite.
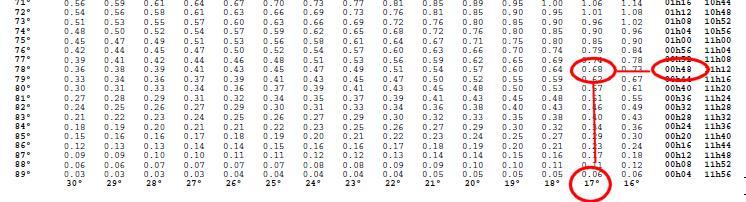
Comme (m+n) est négatif, on compte à partir du pôle abaissé.
L'angle horaire local est compris entre 0° et 180°, on porte donc l'azimut vers l'ouest.
On lit donc S 17° W, soit 197°.
Les tables HO.249 ont été conçues pour l'aéronautique. C'est l'équivalent américain des AP.3270 britanniques. Elles permettent en une fois d'obtenir la hauteur estimée et l'azimut. Elles sont composées de 3 gros volumes.
Elles doivent cependant utiliser une position estimée différente de la position réellement estimée.
Et il existe de nombreuses autres tables et abaques, de toutes origines, et dans toutes les langues.
Elles ont toutes le même but, et sont toutes aussi fiables, pour peu qu'on sache s'en servir.
Le tout, c'est de trouver celles qu'on préfère, et avec lesquelles on est le plus à l'aise.
Une calculette est électrique..., mais il existe des calculettes qui remplacent les éphémérides et autres almanachs. La très fameuse Tamaya a eu son heure de gloire. Je ne suis pas sûr cependant que les programmes qui y tournent prennent en compte les secondes intercalaires... À vérifier.
Il existe nombre de programmes pour éditer les almanachs et éphémérides, ainsi que pour résoudre les calculs nécessaires pour la navigation astronomique, on en fournira une liste en annexe.
Dans le cadre de ce document, l'aspect qui nous concerne est l'édition des éphémérides.
Des classes Java (et dans plusieurs autres langages) sont disponibles dans un git repository (https://github.com/OlivierLD/ROB/tree/master/astro-computer/AstroComputer). Ce code est basé sur les algorithmes astronomiques de Jean Meeus et le travail remarquable de Hening Umland. Ces classes permettent de calculer les données de l'almanach pour le Soleil, la Lune, quatre planètes (Vénus, Mars, Jupiter et Saturne), ainsi que pour une bonne cinquantaine d'étoiles. On peut aussi par la même occasion calculer les distances entre les astres, en particulier les distances lunaires.
On utilise Java pour générer un fichier XML (eXtensible Markup Language) qu'on transforme ensuite en pdf en utilisant XSL (eXtensible Stylesheet Language) et FOP (Formatting Object Processor), ce qui apporte une grande souplesse à la démarche. On peut éditer ce qu'on veut, dans le format qu'on souhaite. Plusieurs exemples sont donc - disait-on - disponibles sur le site.
Pour les détails sur l'utilisation de ces programmes, voyez sur le site dont l'URL est citée ci-dessus.
On peut aussi générer les tables de calcul (Dieumegard & Bataille), ainsi que les tables d'interpolation, très pratiques. Ces dernières peuvent être générées en quelques clics dans un tableur, c'est réellement spectaculaire. C'est d'autant plus commode qu'il est possible de se réaliser ses propres tables d'interpolation, en fonction de ses besoins.
Les calculs nécessaires pour la navigation astronomique sont longs, c'est le moins qu'on puisse dire. Ils ne sont cependant pas difficiles, et avec un peu de pratique, c'est très facile, et on acquiert très vite une forme de routine. Il ne faut pas hésiter à la pratiquer - à terre et en mer - autant que possible, il est essentiel de ne pas avoir à apprendre cette technique sur le tas, quand le GPS se met en botte... Il convient aussi de ne pas rendre cette routine trop automatique, il convient de persister à savoir ce qu'on fait, afin de pouvoir détecter les erreurs et les aberrations.
Et surtout, c'est sans doute la technique de navigation la plus gratifiante. Quand au terme d'une traversée on dit à l'équipage "On devrait voir une terre devant nous dans environ une demi-heure", ils ont tous cet air entendu, sur le mode "Mais bien sûr...". Mais quand trente minutes plus tard, la terre apparaît, ils sont sciés, et c'est bien normal.
La donnée la plus difficile à obtenir, c'est l'heure exacte, dont dépend directement le calcul de la longitude.
Lorsqu'elle était encore impossible à obtenir d'un manière fiable, il était courant lors d'un
long voyage - et lorsque c'était possible - de se caler dès que possible sur la latitude d'arrivée.
Le reste du trajet s'effectuait alors d'est en ouest, ou d'ouest en est.
La latitude est comme on l'a vu facile à obtenir, même lorsqu'on ne dispose pas d'un chronomètre suffisamment fiable.
Ainsi, à défaut de savoir quand on allait arriver, on savait où.
De nombreux voyages entre les Amériques et l'Europe ont été effectués de cette façon. Ainsi qu'entre l'Arabie et l'Inde.
C'est une idée Arabe, dont Tim Severin parle dans la relation qu'il fait de son “Voyage de Simbad”.
Le Kamal est un instrument rudimentaire, utilisé pour évaluer la hauteur d'un astre - des étoiles en
particulier - lorsqu'il passe à son point le plus bas.
Plus qu'une méthode de détermination de la longitude, c'est en fait une façon de recaler le chronomètre, ce qui mène
à la détermination de la longitude. Joshua Slocum y fait référence.
Le principe est simple, il exploite le mouvement très particulier de la Lune par rapport aux autres astres visibles.
Elle est en effet l'astre visible dont le mouvement propre est le plus flagrant.
La Lune a de nombreuses caractéristiques uniques, son mouvement propre fait qu'on a l'impression
qu'elle se déplace à l'envers dans le ciel...
Son mouvement propre est précisément ce qui constitue son intérêt ici.
Un autre aspect important de cette méthode - si ce n'est la raison pour laquelle elle existe, c'est que - une fois corrigée - l'observation faite d'une distance entre deux astres ne dépend pas (ou très peu) de la position géographique de l'observateur.
Dans la voûte céleste, les astres visibles (Soleil, planètes, étoiles) seront considérés comme les chiffres
d'une grande pendule, où la Lune jouerait le rôle de la grande aiguille.
Le problème, c'est que les chiffres bougent aussi. Mais ça fonctionne.
On utilise alors le sextant, non plus pour mesurer une hauteur sur l'horizon, mais une distance entre deux astres.
On choisira pour mesurer cette distance des astres situés au voisinage du trajet de la Lune dans la ciel,
de façon à ce que la distance qui nous intéresse varie de manière substantielle avec le temps.
Par exemple, l'étoile Polaire ne sera d'aucune utilité...
Ça marche, mais il faut savoir quel crédit accorder à cette méthode.
Si on considère par exemple la mesure de la distance Lune-Soleil, cette distance varie par heure d'environ 30'.
Une erreur d'une minute d'arc sur le sextant - et cette mesure est plus difficile à obtenir que dans le cas d'une
hauteur sur l'horizon - correspond à une erreur de temps de l'ordre deux minutes...
On fait en général plusieurs observations, dont on calcule ensuite une moyenne.
Il faut pouvoir mesurer la distance lunaire avec une précision inférieure à une minute d'arc.
C'est une méthode délicate, qui requiert beaucoup de précision, et beaucoup de calculs.
Mais encore une fois, ça marche. On n'en attendra pas cependant la précision qu'on peut obtenir avec un droite de hauteur.
La fourchette d'erreur est de l'ordre de plusieurs dizaines minutes de longitude...
Mais à nouveau, cette méthode a été développée alors que les chronomètres n'étaient pas disponibles.
Et une longitude qui comporte une erreur de 30 minutes vaut mieux que pas de longitude du tout.
Une étape importante de la mesure d'une distance lunaire (au même titre qu'une distance entre deux astres,
qu'il s'agisse de la Lune ou pas), c'est la correction de la mesure effectuée avec le sextant.
La correction de cette fameuse distance est effectuée à l'aide de la formule de Young :
Hm est la hauteur de la Lune (Height Moon)Hb est la hauteur de l'autre corps céleste (Height Body)Dapp est la distance apparenteHmapp est la hauteur apparente de la LuneHbapp est la hauteur apparente de l'autre corps célesteIl est indispensable pour atteindre la précision requise de recourir aux logarithmes. Ce qui complique notoirement la procédure.
Bruce Stark a conçu de nouvelles tables destinées à corriger la distance observée. Avec les almanachs qu'on trouvera en annexe, on pourra diviser la quantité de calculs par deux, puisqu'on y fournit les distances lunaires pour plusieurs astres, assorties de différences tabulaires. Et pendant qu'on y était, on a aussi ajouté la parallaxe horizontale lorsqu'elle a un sens, à savoir pour la Lune, le Soleil, Vénus et Mars.
Note : En plus de mettre en œuvre une grande quantité de calculs, cette méthode requiert la valeur de la distance d'un
astre avec la Lune, qui se trouve être aussi délicate à mesurer.
Quand on mesure la hauteur d'un astre au-dessus de l'horizon, on part le l'astre, qu'on "descend" sur l'horizon, lequel est difficile à louper.
Dans le cas des arcs capables, idem ; on part d'un amer, on va forcément croiser l'autre.
Ici, on part d'un astre, et on "vise" un autre point dans le ciel. Le sextant n'est ni vertical, ni horizontal (ou alors exceptionnellement) ;
on n'est pas sûr de ne pas dépasser le deuxième astre sans le voir...
Encore une fois, il faut un peu d'entrainement pour être à l'aise avec cette technique. Il faut s'y mettre avant d'y être confronté !
Cette section détaille des points évoqués précédemment dans le document.
Ça devrait en général amuser ceux qui n'écoutaient pas en math...
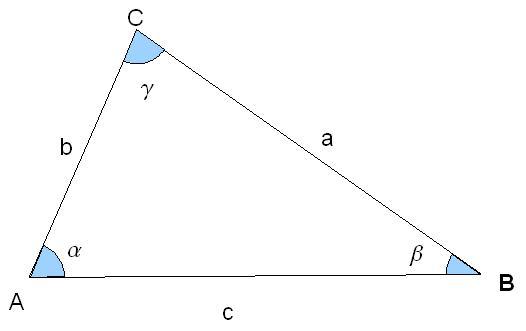
a, b et c sont connus, on veut la valeur des angles α, β et γ.
Il s'agit de démontrer que le lieux des points qui interceptent un segment sous le même angle est un cercle.
On procède en deux étapes.
On veut d'abord démontrer que β = 2 × α.
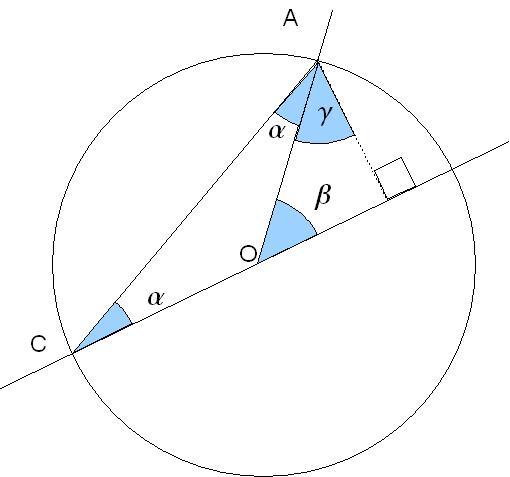
O est le centre du cercle, donc la longueur OC est égale à la longueur OA,
donc le triangle OAC est isocèle. Donc son angle en C est égal à son angle en A.
AB est constant, l'angle α + β est invariant.
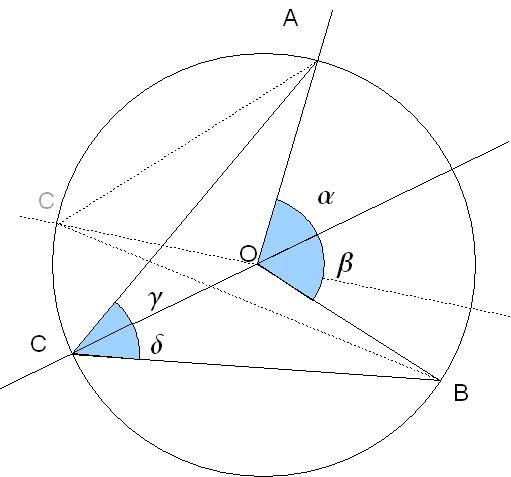
C sur le cercle, la somme γ + δ est égale à la moitié de (α + β).
La "Latitude Croissante" est le fondement de la construction des cartes Mercator.
On rappelle que l'intérêt majeur de la projection de Mercator est de représenter un cap constant
entre deux points de la carte par une droite (loxodromie), ce qui n'est pas vrai pour les autres projections.
C'est fort loin d'être aussi trivial que ça en a l'air... Une carte est plate, la Terre est sphérique...
Mercator était un géographe flamand né le 5 mars 1512.
Pour la latitude φ, λ est la latitude croissante de φ, exprimée en radians.
On rappelle que Π/4 radians = 45°. Et tan(Π/4) = 1. Ln(1) = 0.
C'est donc la formule qu'on utilise pour construire les cartes Mercator.
À nouveau, ces cartes présentent l'intérêt majeur de représenter les loxodromies par des lignes droites.
Quand bien même le problème paraitrait simple, la solution n'est pas complètement triviale (voir ci-dessus) !
À l'aide de cette formule, il est possible de réaliser des canevas Mercator, fort commodes lorsqu'on fait un point par droites de hauteur. De tels canevas, réalisés à l'aide de cette formule sont fournis dans un document séparé.
Les cartes de Mercator ne peuvent pas représenter les pôles, qui ont du fait de la formule utilisée une latitude croissante infinie (tan(90°)=∞). La latitude croissante exprime en fait l'échelle à considérer - le rapport entre un degré de latitude et un degré de longitude - à une latitude donnée.
Exemple : Latitude croissante de 45°. Dans la formule ci-dessus, on a donc φ=45°. On cherche d'abord tan(67.5°), on trouve 2.41421. Le logarithme népérien de cette valeur est 0.88137, qu'on convertit de radians en degrés pour trouver 50.498986°, soit 50°29.94'.
Ceci signifie qu'à une latitude de 45°, la représentation sur une carte Mercator de cette valeur à la taille de 50°29.94' de longitude.
La figure suivante illustre le calcul précédent.
Notez aussi la dilatation de l'échelle de latitudes au fur et à mesure qu'on s'approche du pôle. Les pôles sont à l'infini sur une carte Mercator.
Les canevas Mercator sont des cartes vides, mais qui respectent - pour une latitude donnée - cette notion de "Latitude Croissante".
À l'équateur, la projection est presque carrée, à 50° de latitude, ces "carrés" sont nettement plus hauts que larges.
Pour reporter les distances sur un canevas Mercator, on utilise - comme sur n'importe quelle carte Mercator -
les côtés verticaux de la carte. D'où l'intérêt de ces canevas.
Les "Plotting Sheets" remplissent le même rôle que les canevas Mercator, et sont au moins aussi pratiques.
Voici une des ces Plotting Sheets, vide elle aussi.
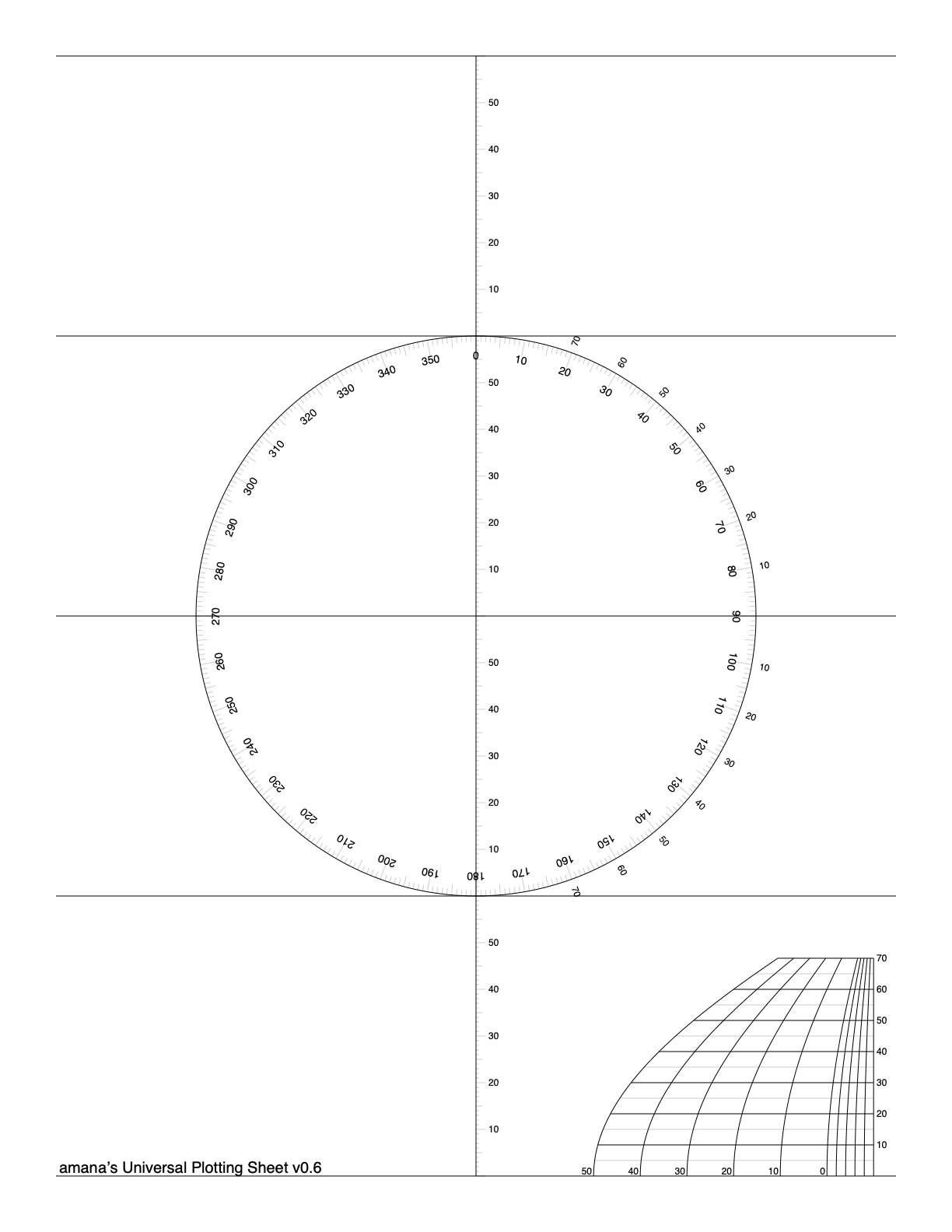
Comme on l'a vu, c'est une donnée corrélée au temps de passage au méridien. On verra aussi pourquoi on continue de parler de temps de passage au méridien et d'équation du temps.
Le fait est que le soleil ne passe pas au méridien à midi, alors qu'on serait tenté de penser que c'est
pourtant la définition de ce que midi devrait être. Voici pourquoi :
La terre tourne sur elle-même de 360 degrés en 24 heures.
En outre, elle se déplace autour du soleil, dont elle fait le tour en quelque chose comme 365,25 jours.
Et c'est là que c'est intéressant.
Un petit dessin vaut mieux qu'un long discours, d'autant mieux qu'on exagère l'échelle du problème.
Le temps de passage à Greenwich est donné dans les éphémérides. Ce temps de passage évolue d'un jour à l'autre, et nécessite une interpolation si on cherche le temps de passage d'un astre à une autre longitude que celle de Greenwich.
L'équation du temps est en fait la différence qu'il existe entre le midi local et le temps de passage d'un astre.
Cette équation du temps peut être interpolée, tandis que le temps de passage à Greenwich ne saurait être
autre chose que le temps de passage... à Greenwich.
En effet, le temps de passage à Greenwich évolue de jour en jour. La grandeur qui change - de manière continue - est
appelée l'"équation du temps".
Pour formuler le problème autrement, essayez de répondre à cette question :
"Comment est-ce que le temps de passage à Greenwich pourrait bien varier en fonction de la longitude ?"
C'est pourquoi cette notion d'équation du temps a été introduite, pour lever cette ambiguïté engendrée par l'interpolation du temps de passage à Greenwich.
Les tables de logarithmes (aka "tables de log") sont des documents imprimés qui permettent de résumer des opérations complexes
(multiplication de sinus d'arc-tangentes, et autres salades de la même farine), à des additions et des soustractions,
minimisant par là même les occasions de faire des erreurs de calcul.
En tant que document imprimé, ça ne tombe pas en panne en cas de coupure de courant, d'où son intérêt ici.
Leur usage n'est cependant pas toujours complètement intuitif..., d'où ce paragraphe.
Ceci est plutôt un exercice de style... Ou alors destiné à ceux qui auraient oublié
leurs tables (Dieumegard et Bataille) de calcul, et pas leurs tables de log ; ce qui est improbable, certes.
C'est néanmoins intéressant, d'autant plus que ça fonctionne, et que ça a
longtemps été la seule option disponible.
Le nombre des étapes du calcul (dont chacune peut donner lieu à des erreurs), et la complexité du processus sont
précisement ce qui a donné lieu à l'élaboration des tables de calcul comme celles de Dieumegard & Bataille.
Rien de nouveau ici, et c'est toujours valable - en informatique par exemple. Moins on écrit de code (plus il est concis), moins il y a de bugs.
Les tables donnent les logarithmes décimaux (et non pas népériens, ainsi qu'on les utilise en math).
x=x'.10n,
où x' est un réel supérieur ou égal à 1, et inférieur à 10.
c,m , où "c" est
la caractéristique, et "m" la mantisse.
"c" est un nombre entier"m" est un nombre réel positif ou null, strictement inférieur à 1"," est le séparateur décimal (ce qui n'est pas vrai partout, ça peut aussi être un point)"1,2345", la caractéristique est "1", la mantisse est "0,2345".
Donc, $ x' \in \mathbb{R} \cap [1, 10[, log(x') \in \mathbb{R} \cap [0, 1[ $
en conséquence :
log(x) = n + mantisse
log(x) = n + 0,......
Attention !! Caractéristiques négatives !. C'est très pratique mais il faut être prévenu.
0,1234
+ 1,2345
+ 2,3456
On trouve bien évidemment
3.7035
Mais si on pose
0,1234
- 0,7655
+ 2,3456
On veut trouver 1,7035, certes, mais c'est moins facile, davantage d'erreurs sont possibles, surtout si ça souffle...
-0,7655 = 0,2345 - 1 (ou -1 + 0,2345), on notera 1,2345 :
0,1234
+ 1,2345
+ 2,3456
On fait une addition des mantisses, mais en retranchant les valeurs surlignées lors de l'addition des caractéristiques.
Plus en détails, pour être sûr :
Pour les mantisses, on continue comme avant de les additionner, avec - s'il y a lieu - des retenues :
0,1234
+ 1,2345
+ 2,3456
----------
...,7035
Pour les caractéristiques, on soustrait celles qui sont négatives :
0,....
- 1,.... (surligné, donc négatif ! )
+ 2,....
--------
1,....
On assemble les résultats obtenus, caractéristique (1) et mantisse (7035) : 1,7035.
0,1234
+ 1,2345
+ 2,3456
----------
1,7035
|
0,1234
- 0,7655
+ 2,3456
----------
1,7035
|
La table donne les logarithmes de nombres de 1 à 10.
On est en log décimaux, donc
log 101 = 1
log 102 = 2
log 103 = 3
etc.
Avant de procéder, afin de pouvoir utiliser la table, il est donc nécessaire de réduire le nombre dont on cherche le logarithme à un nombre compris entre 1 et 10, et d'en préserver la caractéristique.
Exemple :
Recherche du logarithme d'un nombre à 4 chiffres : log(2745).
2745 = 2,745.103
donc log(2745) = 3 + log(2,745)
On cherche donc dans la table, non pas 2,745, mais 2745.
274 dans la colonne de gauche, et le dernier chiffre - 5 - dans une colonne de la table.
Le log de 2,745 est à l'intersection de la ligne 274 et de la colonne 5.
log(2,745) = 0,43854.
Donc, log(2745) = 3,43854.
De la même manière, on cherche le logarithme de 0,2745.
0,2745 = 2,745.10-1, la valeur à chercher dans la table demeure la même.
Donc log(0,2745) = -1 + log(2,745), soit 0,43854 - 1, soit -0,56146.
Autre exemple : log(2,517) = ?
Exemple :
Recherche de la valeur de log(28,864).
Comme précédemment, on réduit à un nombre situé entre 1 et 10 :
Log (28,864) = log(2,8864.101)
Ensuite on situe ce nombre entre deux valeurs à 4 chiffres :
2,886 < 2,8864 < 2,887
De la table, on détermine :
log(2,886) = 0,46030
log(2,887) = 0,46045
La différence entre les deux valeurs des logarithmes est 0,00015, soit 15 cent-millièmes.
Posé autrement:
0,46030
+ 6,0
----------
0,46036
Ainsi, log(28,864) = 1,46036.
Logarithme des fonctions trigonométriques :
Il n'est pas nécessaire ici de réduire la valeur du nombre à chercher. La table donne la valeur
des fonctions trigonométriques usuelles pour des valeurs d'angles pré-définis. La précision
est en général de l'ordre de la minute d'arc, certaines tables vont jusqu'à la seconde d'arc.
Ce dont il convient de se préoccuper en priorité, c'est du système de notation
employé, caractéristique surlignée, ou 10 à soustraire de de la valeur.
Il est facile de discerner le système de notation utilisé, si on se souvient que les
sinus et cosinus sont forcément compris entre -1 et +1. Un coup d'œil suffit pour savoir si dans leurs cas,
la caractéristique est surlignée, ou supérieure à 1.
C'est la méthode la plus générique - et la plus longue - puisqu'elle résout littéralement les formules,
mais qui marche partout avec un minimum de matériel. Rien ici n'est dédié à ce type de calculs.
Il s'agit surtout ici de démontrer la validité de la méthode.
Ceci peut être vu plutôt comme un exercice de style...
Ceux qui ne veulent pas s'encombrer avec des logarithmes (ou qui n'écoutaient pas en math) peuvent aller directement à la section Avec des tables de navigation.
Ceux que ça persiste à intéresser peuvent se rafraîchir la mémoire au sujet de la manipulation de ces ustensiles dans la section précédente, Utilisation simplifiée des tables de logarithmes.
Avec une table de logarithmes, le calcul d'une hauteur comporte 12 étapes, et le calcul de l'azimut en comporte 12 également.
À vos marques !
Pour ceux que la manipulation de ces tables intéresse, on fournit ici une page qui permet de valider ses résultats, étape par étape.
Comme déjà mentionné, on cherche donc à résoudre litéralement les formules suivantes :
On donc veut résoudre
On va donc rechercher les logarithmes de :
sin(L) = sin(37°46')
sin(D) = sin(-6°10.84') arrondi à sin(-6°11')
cos(L) = cos(37°46')
cos(D) = cos(-6°10.84') arrondi à cos(-6°11')
cos(AHL) = cos(12°26.5') arrondi à cos(12°26')
log sin(37°46') = -0.21293log sin(6°11') = -0.96734 (Note: on prend la valeur absolue de l'angle)log cos(37°46') = -0.10209log cos(6°11') = -0.00253log cos(12°26') = -0.01031log (sin(L).sin(D)) = -0.21293 - 0.96734 = -1.18027sin(L).sin(D) = 0.065795log(cos(L).cos(D).cos(AHL)) = -0.10209 - 0.00253 - 0.01031 = -0.11493cos(L).cos(D).cos(AHL) = 0.7675sin(L).sin(D) + cos(L).cos(D).cos(AHL) = 0.701705log(0.701705) = log(7.01705.10-1) = log(7.01705) - 1 = 0.846192.10-1He = 44°33.5'
Voyons maintenant comment en arriver là.
Afin de pouvoir s'adresser au plus grand nombre, on fera ces calculs à l'aide de
Le but de ces tables est strictement identique, mais les conventions qu'elles utilisent sont parfois différentes,
et méritent d'être évoquées.
Une différence importante concerne la façon d'afficher les valeurs négatives des logarithmes.
Un gros avantage des tables de logarithmes est de réduire multiplications et divisions à des additions et soustractions.
Parmi les membres d'une addition, des valeurs négatives peuvent être à l'origine d'erreurs, d'où les différentes options prises par
les auteurs des tables pour tenter d'éclipser cette difficulté.
Par exemple :
log(sin(37°46')), dont la valeur est -0.21293.
9.78707, à lire 9.78707 - 101,78707, à lire 0.78707 - 1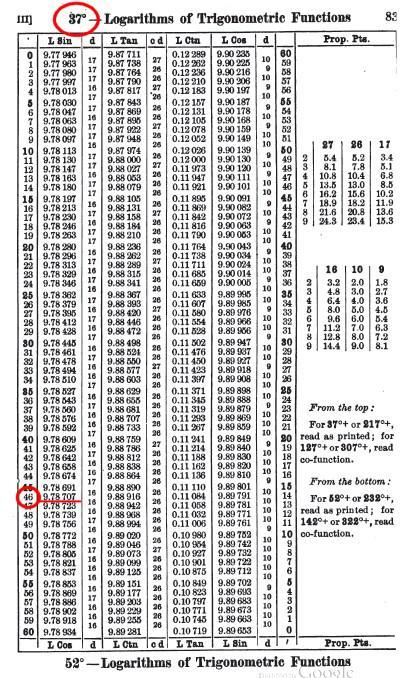
log(sin(37°46')) = 9.78707 soit 9.78707 - 10 = -0.21293
log(sin(6°11')) = 9.03226 soit 9.03226 - 10 = -0.96774
log(cos(37°46')) = 9.89791 soit 9.89791 - 10 = -0.10209
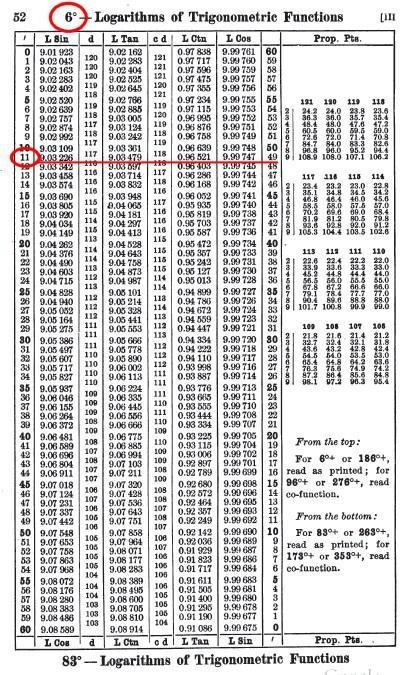
log(cos(6°11')) = 9.99747 soit 9.99747 - 10 = -0.00253
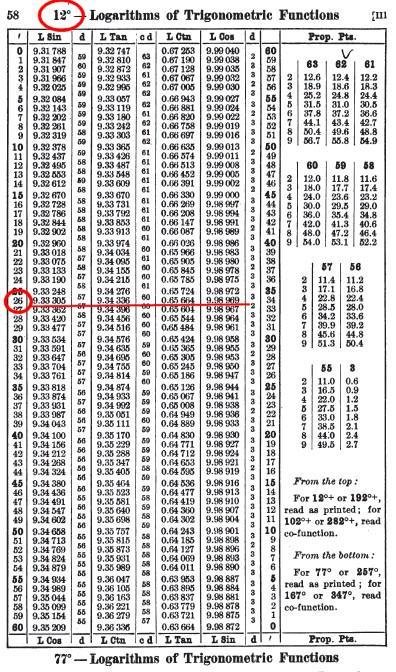
log(cos(12°26')) = 9.98969 soit 9.98969 - 10 = -0.01031
log(sin(L).sin(D)) = -0.21293 - 0.96734 = -1.18027.
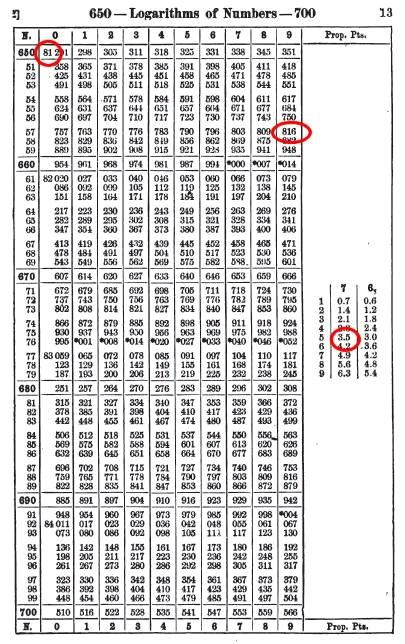
sin(L).sin(D) = 10(-1.18027)=10(0.81973 - 2)=6.5795.10-2=0.065795
sin(L).sin(D) = -0.065795.
log(cos(L).cos(D).cos(AHL)) = -0.10209 - 0.00253 - 0.01031 = -0.11493.
cos(L).cos(D).cos(AHL) = 10(-0.11493) =
10(0.88507 - 1) =
7.675.10-1 =
0.7675
.
sin(L).sin(D) + cos(L).cos(D).cos(AHL) = -0.065795 + 0.7675 = 0.701705.
log(0.701705) = log(7.01705.10-1) = log(7.01705) - 1.
0.846192 10-1, noté 9.846192 pour la trigonométrie.
9.846192) dans la partie de la table consacrée à la trigonométrie, dans la colonne "sinus".
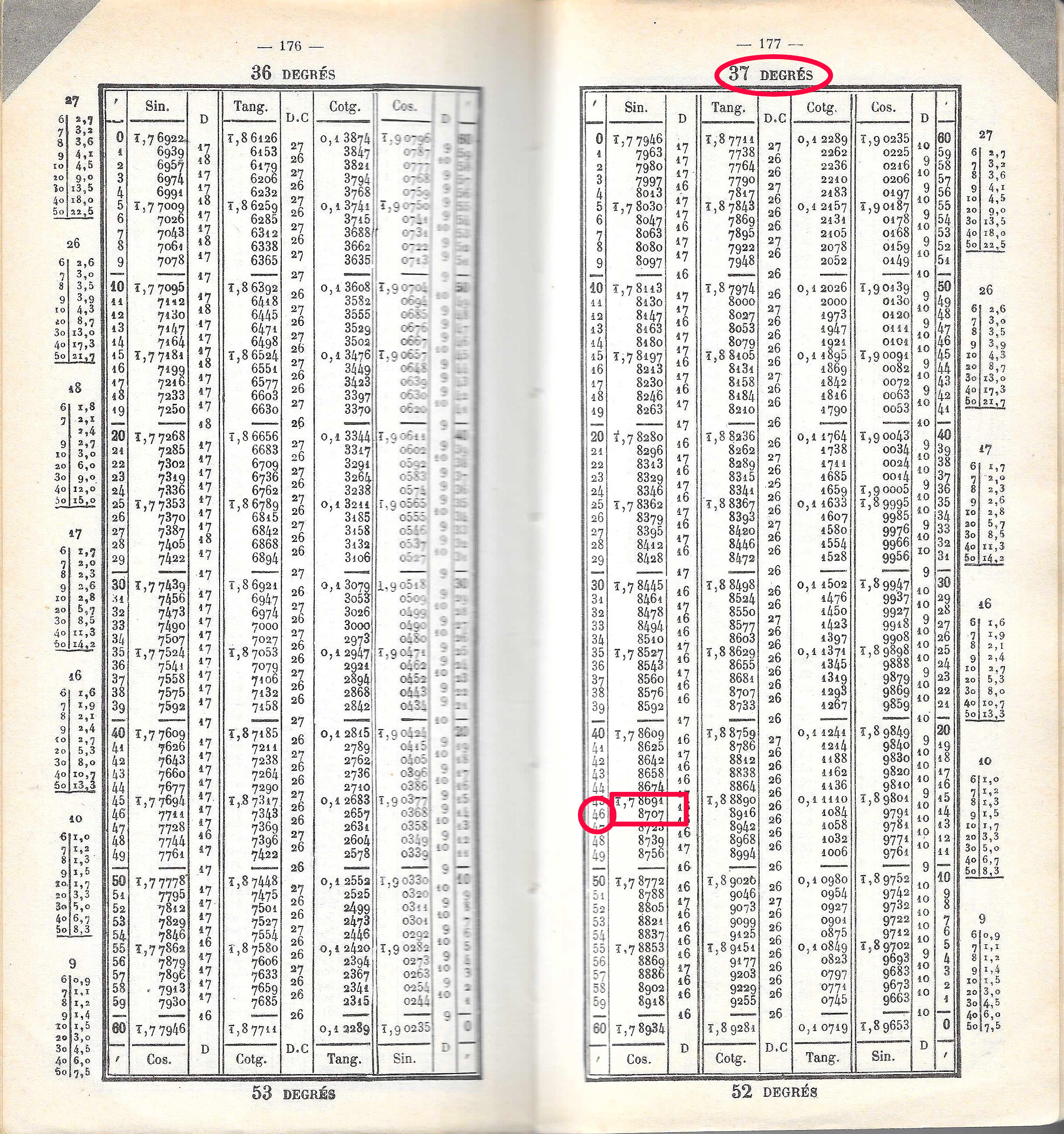
log(sin(37°46')) = 1,78707 (notez la caractéristique surlignée) soit cette fois-ci -1 + 0.78707 = -0.21293
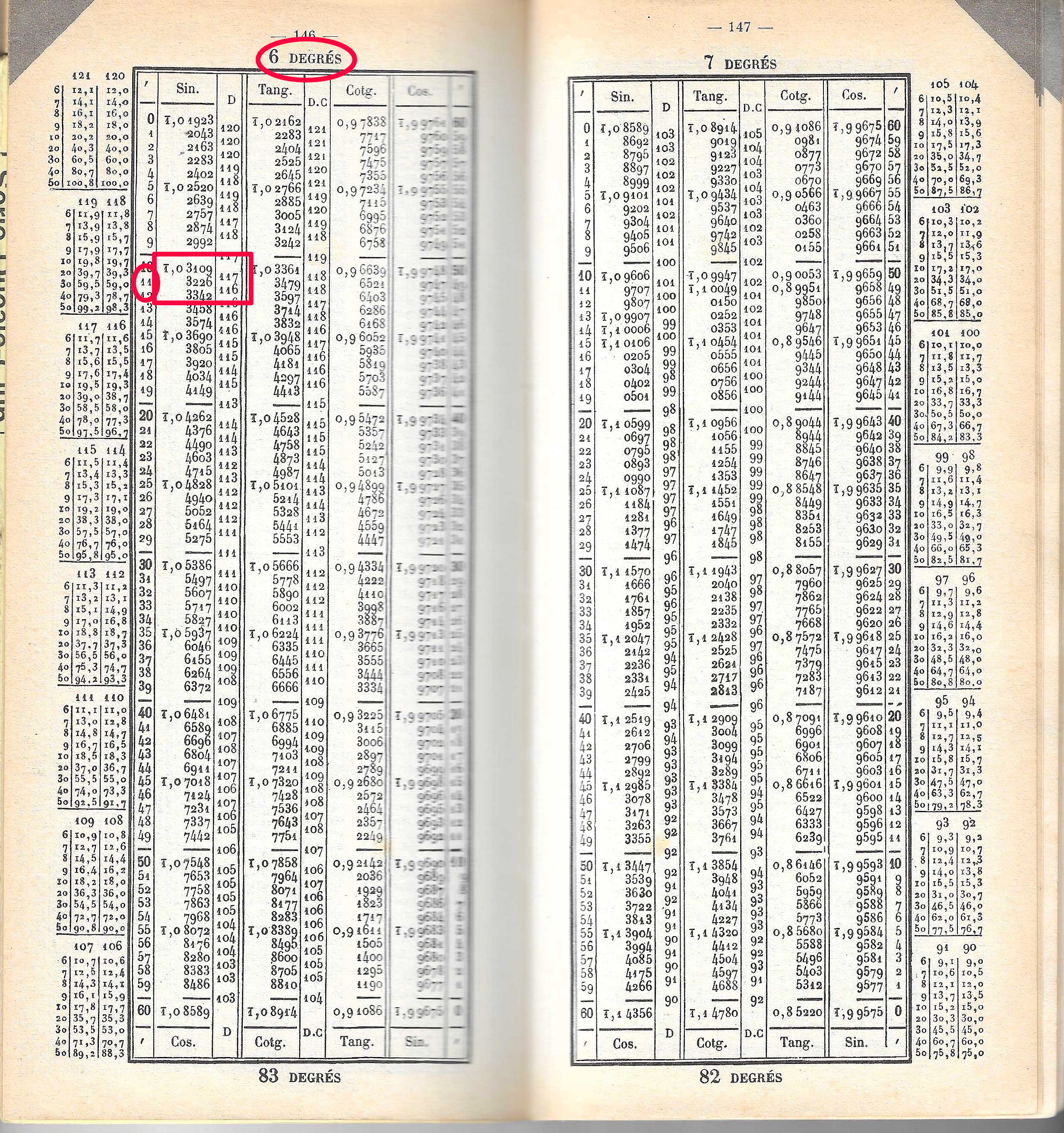
log(sin(6°11')) = 1,03226 (notez la caractéristique surlignée) soit cette fois-ci -1 + 0.03226 = -0.96774
log(cos(37°46')) = 1,89791 (notez la caractéristique surlignée) soit cette fois-ci -1 + 0.89791 = -0.10209
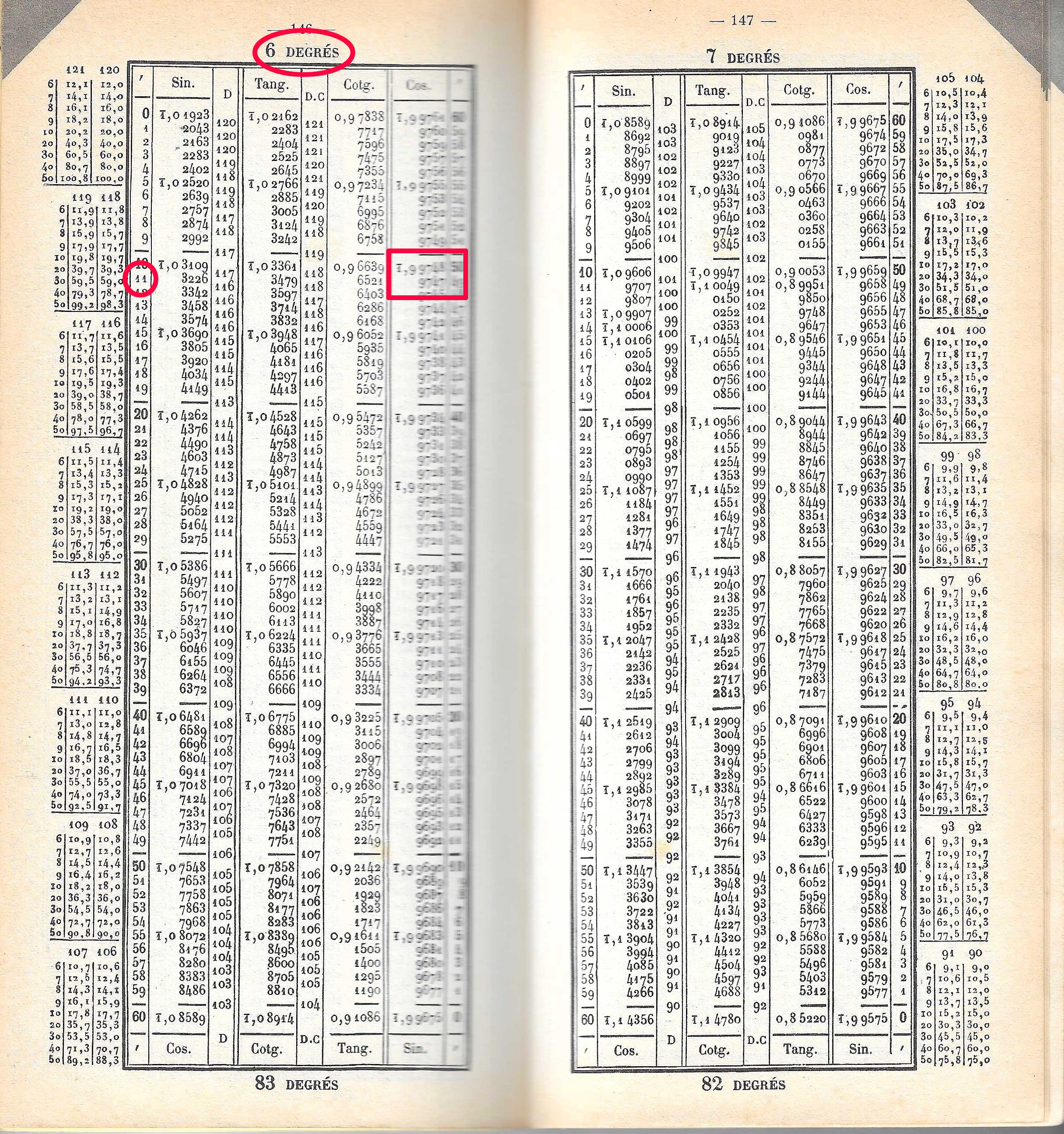
log(cos(6°11')) = 1,99747 (notez la caractéristique surlignée) soit cette fois-ci -1 + 0.99747 = -0.00253
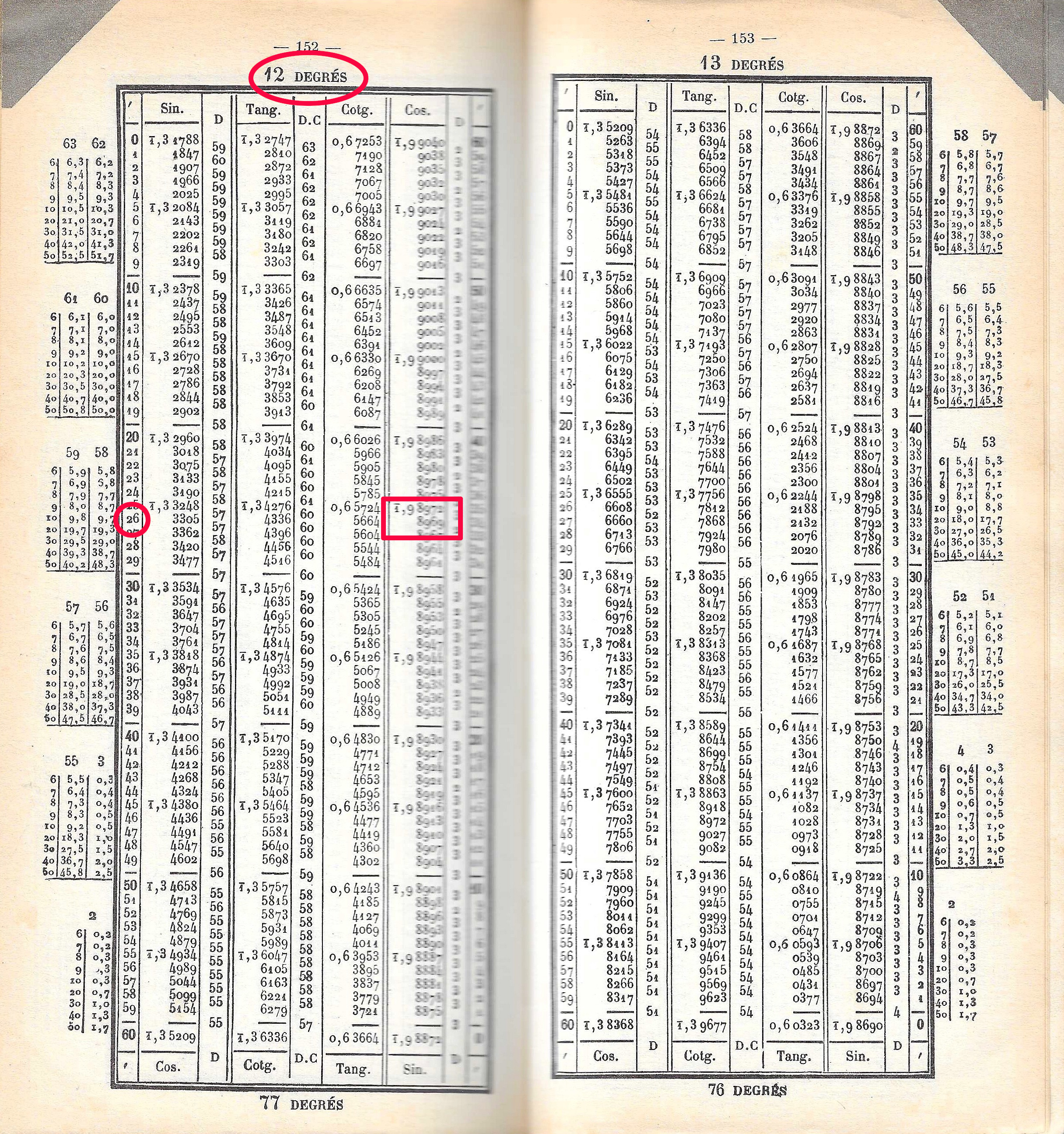
log(cos(12°26')) = 1,98969 (notez la caractéristique surlignée) soit cette fois-ci -1 + 0.98969 = -0.01031
log(sin(L).sin(D)) = -0.21293 - 0.96774 = -1.18067.
1,78707 1,03226 -------- 0,81933On additionne les caractéristiques - celles qui sont surlignées sont négatives, on trouve
-2, le résultat final
est ainsi 0,81933 - 2, soit -1.18067.0,81933 - 2, afin d'avoir un nombre compris entre 0 et 1, -2 sera la puissance de 10.
0,81933 est le logarithme.
N = 650 on a 81 291.N = 659 on a 81 928 dans la 6e colonne, le prochain est 81 935 ⇒ différence tabulaire (935 - 928) = 7.6e colonne, on a maintenant N = 6596.81 933, 5 au dessus de 81 928, on trouve 3,5 dans la petit table de droite DT 7.N = 659635, lu 6,59635.sin(L).sin(D) = 10(-1.18067)=10(0.81933 - 2)=6.5935.10-2=0.0659635
sin(L).sin(D) = -0.0659635.
log(cos(L).cos(D).cos(AHL)) = -0.10209 - 0.00253 - 0.01031 = -0.11493.
1,89791 1,99747 1,98969 -------- 2,885073 caractéritiques à
1 surlignées, 2 de retenue, ça fait (-3 + 2 = -1), on a donc finalement 10(0.88507 - 1)
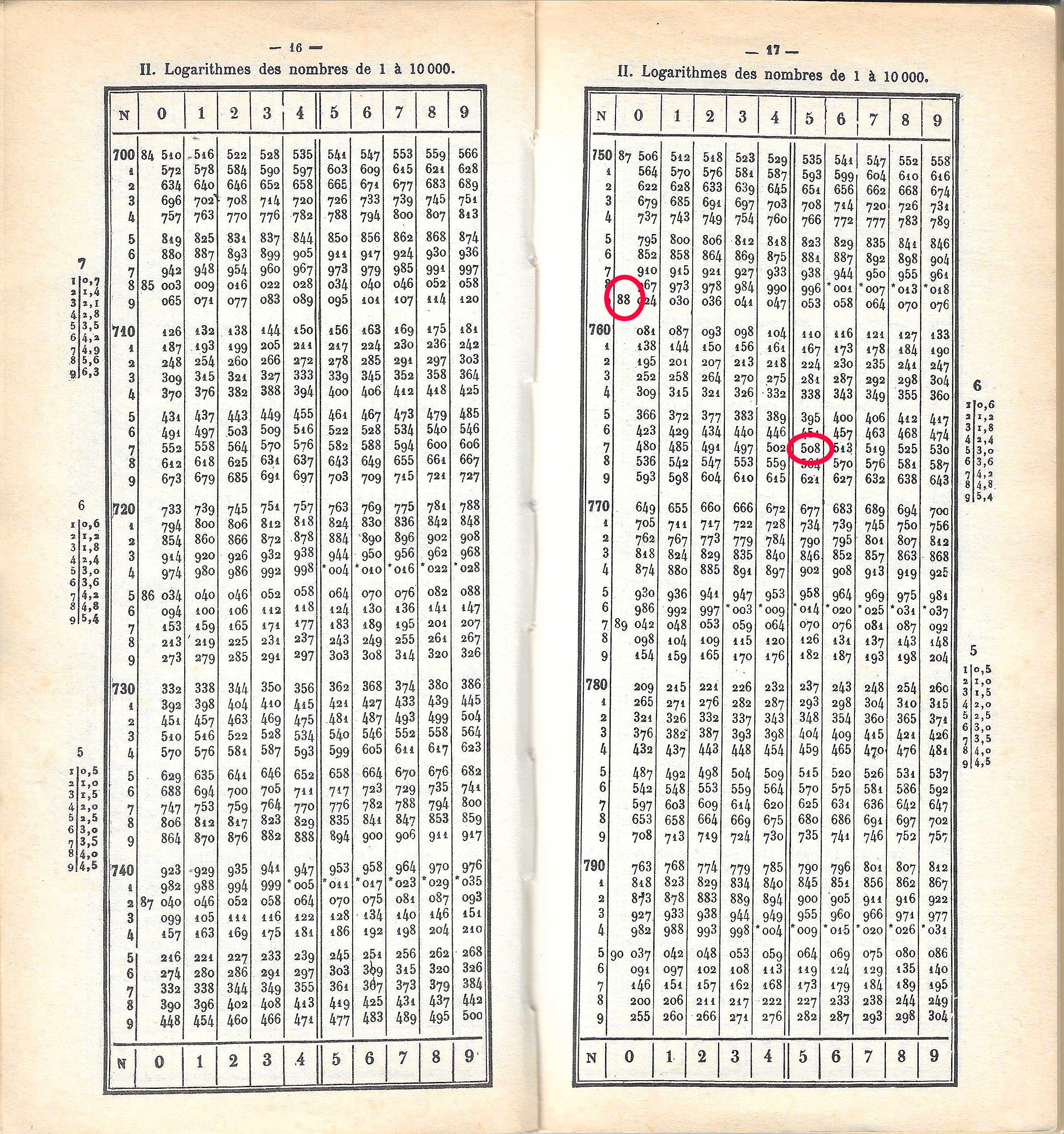
N = 767 pour 88508, dans la 5e colonne, on prendra donc N = 7675.cos(L).cos(D).cos(AHL) = 10(-0.11493) =
10(0.88507 - 1) =
7.675.10-1 =
0.7675
.
sin(L).sin(D) + cos(L).cos(D).cos(AHL) = -0.0659635 + 0.7675 = 0.7015365.
log(0.7015365) = log(7.015365.10-1) = log(7.015365) - 1.
0.84603 10-1.
0.84603 10-1, soit 1,84603) dans la partie de la table consacrée à la trigonométrie, dans la colonne "sinus".
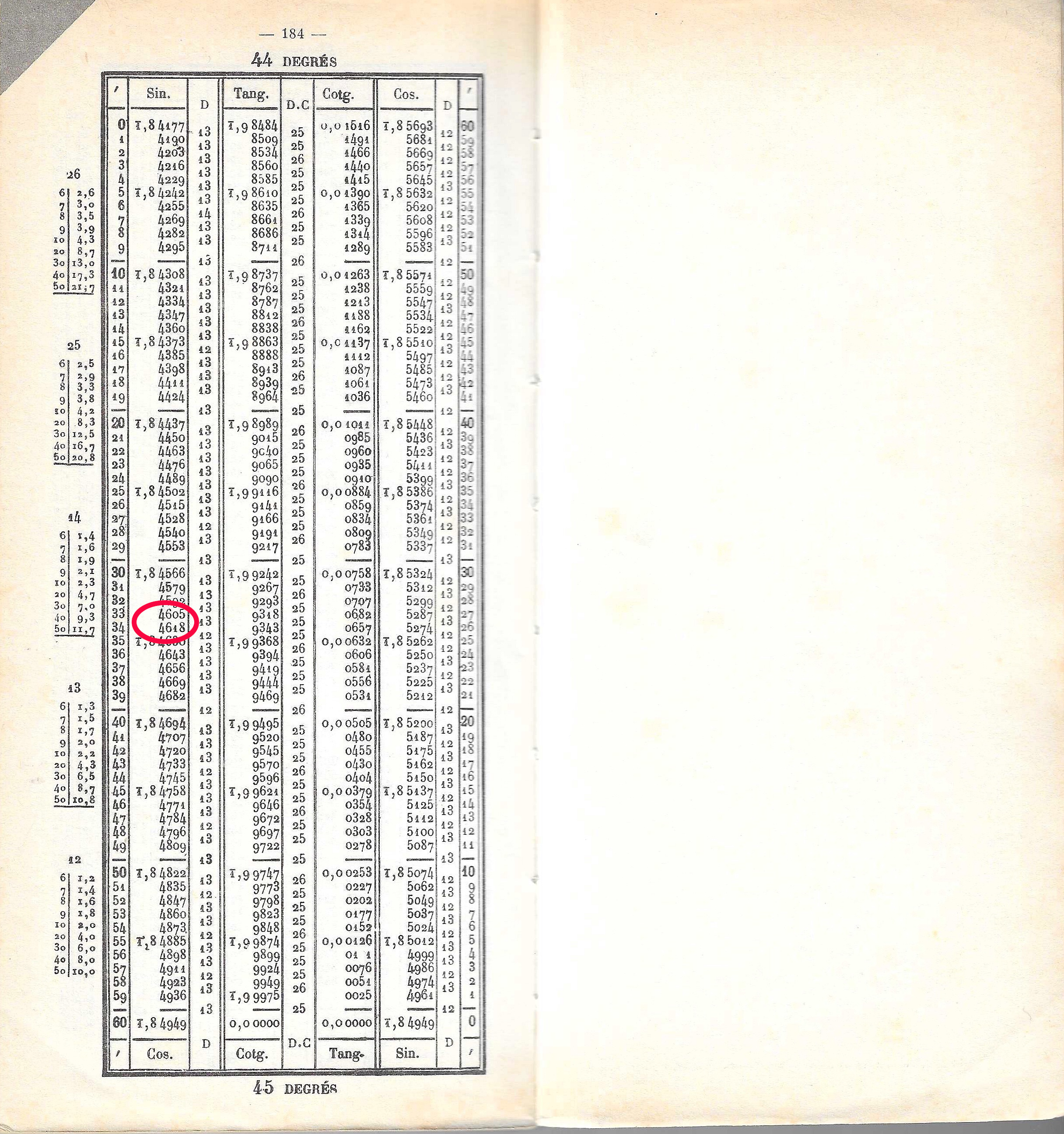
1,84605 dans la table, pour la hauteur estimée He 44°33'.
Cette fois, on veut résoudre
On va donc rechercher les logarithmes de :
sin(AHL) = sin(12°26.5') arrondi à sin(12°26')
sin(L) = sin(37°46') (déjà fait)
tan(D) = tan(-6°10.84') arrondi à tan(-6°11')
cos(L) = cos(37°46') (déjà fait)
cos(AHL) = cos(12°26.5') arrondi à cos(12°26') (déjà fait)
sin(AHL) = sin(12°26.5') arrondi à cos(12°26')
tan(D) = tan(-6°10.84') arrondi à tan(-6°11')
log tan(6°11') = -0.96521log sin(12°26') = -0.66695log cos(37°46') = -0.10209log(cos(L).tan(D)) = -0.10209 -0.96521 = -1.06730 = 0.93270 - 2cos(L).tan(D) = 10(0.93270 - 2) = 100.93270.10-2 = 8.5645.10-2 = 0.085645log sin(37°46') = -0.21293log cos(12°26') = -0.01031log(sin(L).cos(AHL)) = -0.21293 -0.01031 = -0.22324 = 0.77676 - 1sin(L).cos(AHL) = 0.59810log(sin(AHL)) = -0.66695log(arctan(Z)) = 0.49815 - 1Z = 17°29'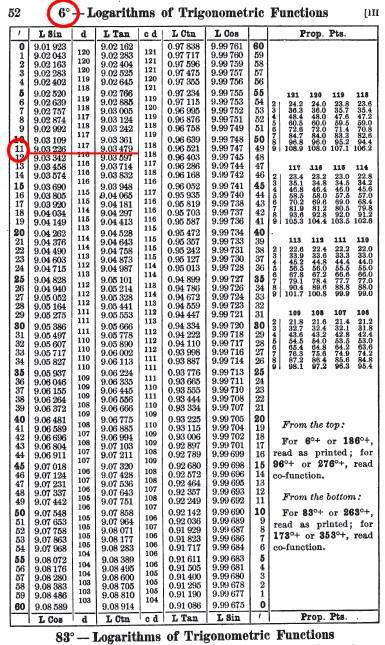
log(tan(6°11')) = 9.03479 soit 9.03479 - 10 = -0.96521
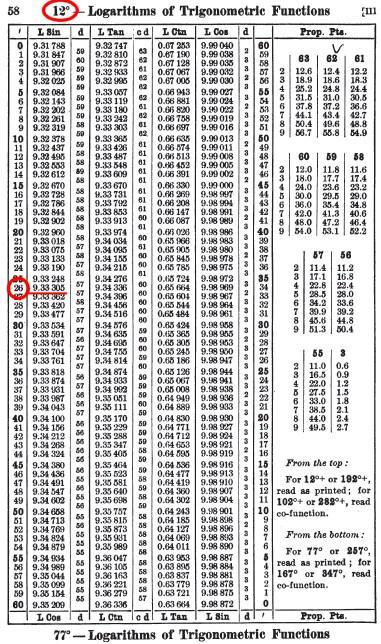
log(sin(12°26')) = 9.33305 soit 9.33305 - 10 = -0.66695
log(cos(L)), c'est -0.10209.
log(cos(L).tan(D)) = -0.10209 -0.96521 = -1.06730 = 0.93270 - 2.
cos(L).tan(D) = 10 (0.93270 - 2) = 100.93270.10-2 = 8.5645 10-2 = 0.085645.
log(sin(L)) = -0.21293, et log(cos(AHL)) = -0.01031
log(sin(L).cos(AHL)) = -0.21293 -0.01031 = -0.22324 = 0.77676 - 1.
sin(L).cos(AHL) = 10(0.77676 - 1) = 100.77676.10-1 = 5.9810.10-1 = 0.59810
log(cos(L).tan(D))−(sin(L).cos(AHL)) devient alors (-0.085645 - 0.59810) = -0.683745.
log(sin(AHL)) = -0.66695.
-0.683745 est-il le logarithme ?
log(0.683745) = log(6.83745.10-1) = 0.834900 - 1 = -0.16510.
log(atan(Z)) = 0.49815 - 1, noté 9.49815 pour la partie des tables consacrée à la trigonométrie.
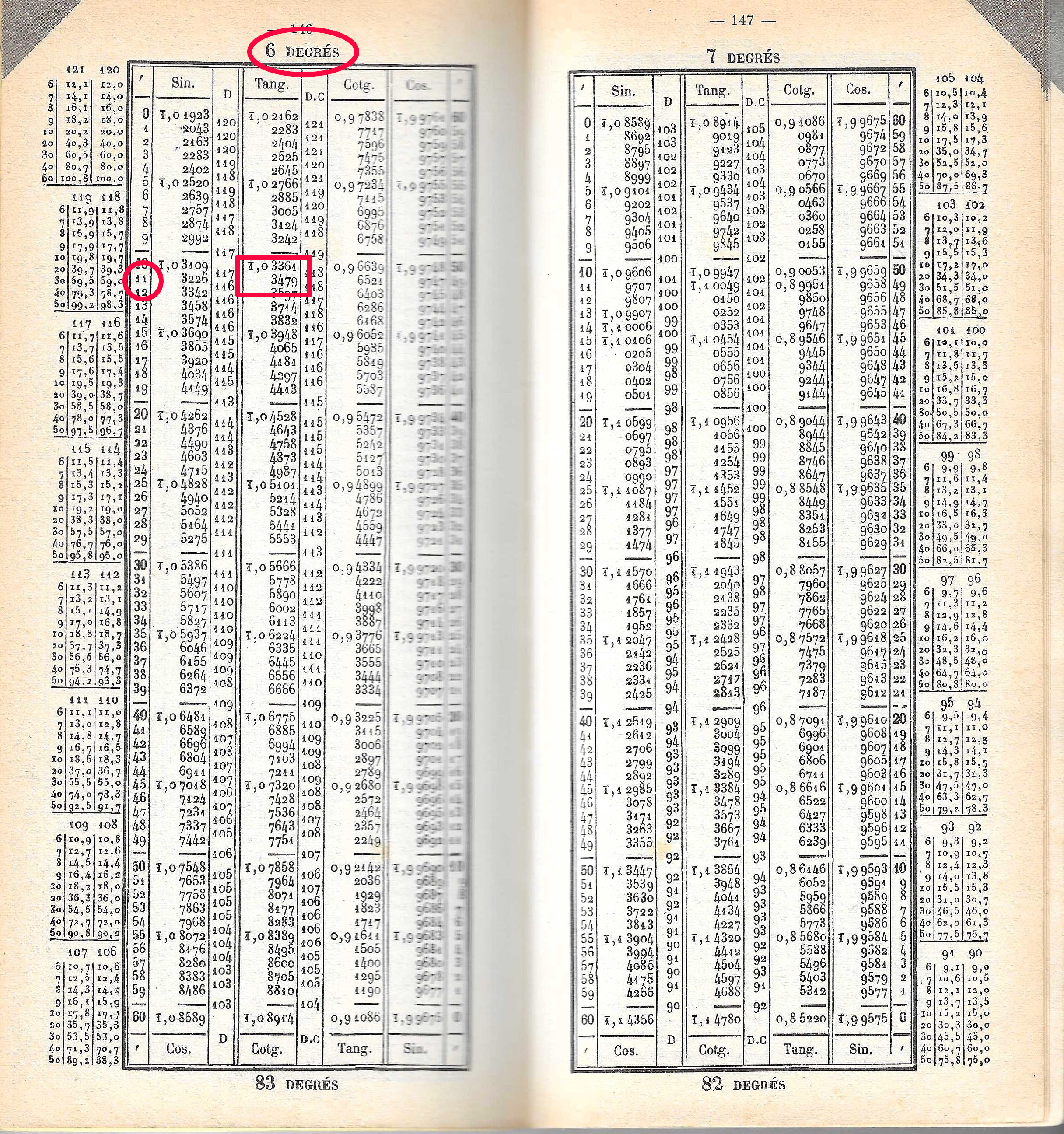
log(tan(6°11')) = 1,03479 soit -0.96521
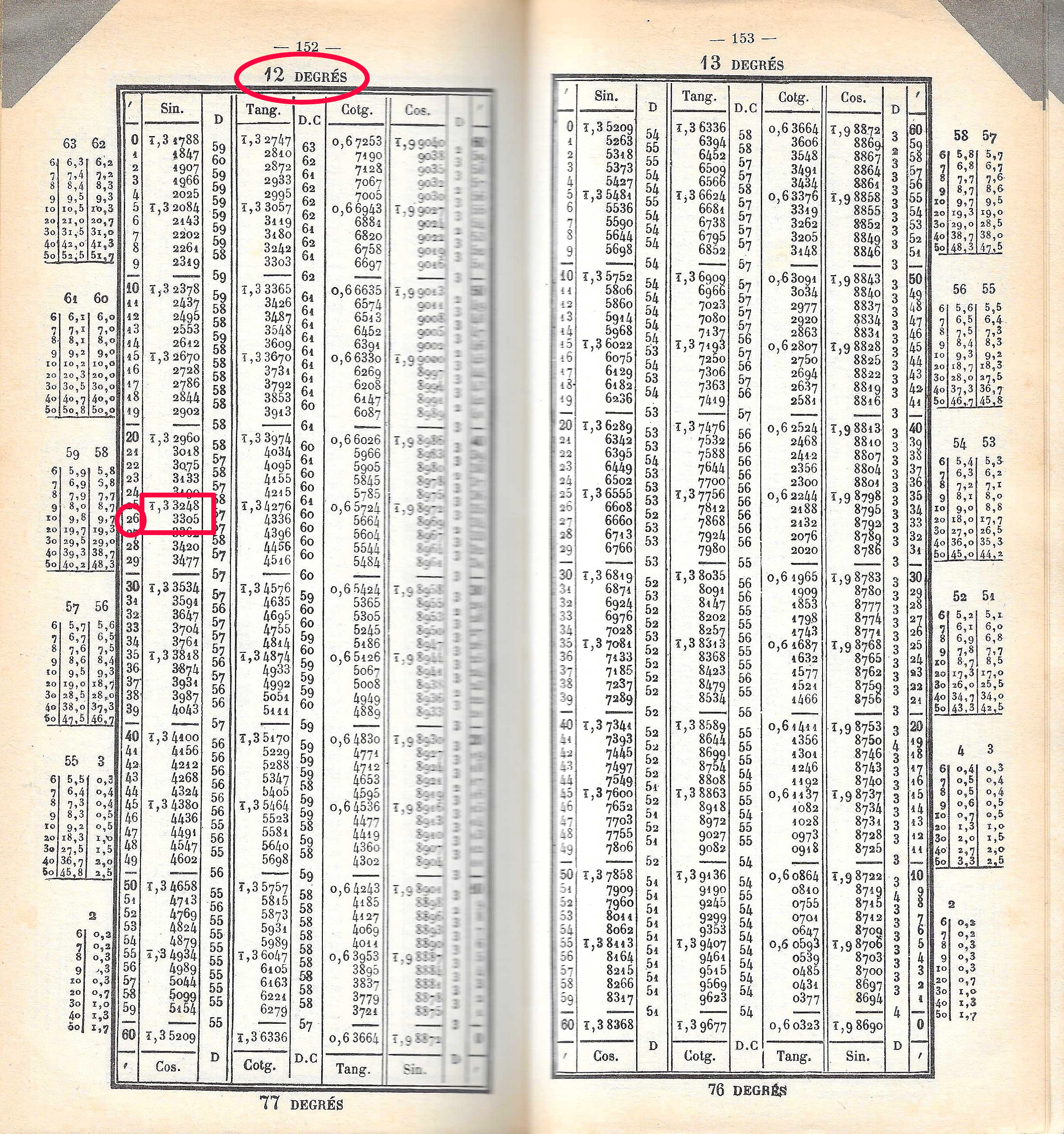
log(sin(12°26')) = 1,33305 soit -0.66695
log(cos(L)), c'est 1,89791, soit -0.10209.
1,89791 1,03479 -------- 0.932702 caractéristiques à 1, surlignées, pas de retenue, ça fait
-1.log(cos(L).tan(D)) = 2,93270 = 0.93270 - 2.
cos(L).tan(D) = 10 (0.93270 - 2) = 100.93270.10-2 = 8.5645 10-2 = 0.085645.
log(sin(L)) = 1,78707 = -0.21293, et log(cos(AHL)) = 1,98969 = -0.01031
1,78707 1,98969 -------- 1.776762 caractéristiques à
1 surlignées, 1 de retenue, ça fait -1.
log(sin(L).cos(AHL)) = 0.77676 - 1.
N = 598 pour 77 677, dans la colonne 1, ça fait 5981.sin(L).cos(AHL) = 10(0.77676 - 1) = 100.77676.10-1 = 5.9810.10-1 = 0.59810
log(cos(L).tan(D))−(sin(L).cos(AHL)) devient alors (-0.085645 - 0.59810) = -0.683745.
log(sin(AHL)) = -0.66695.
-0.683745 est-il le logarithme ?
log(0.683745) = log(6.83745.10-1) = 0.834900 - 1 = -0.16513.
log(atan(Z)) = 0.49818 - 1, noté 1,49818 pour la partie des tables consacrée à la trigonométrie.
Voici un exemple de point par droites de hauteurs.
On utilisera ici une plotting sheet, afin d'illustrer son usage. L'emploi de canevas Mercator
a déjà été évoqué dans la section Ce qu'on cherche.
Pour vérifier vos calculs, on-line :
Ici, on est le 23 octobre 2010, notre position estimée est 0°51.7' N / 138°08.5' W.
On observe Jupiter (♃) et la Lune (son bord inférieur).
Première droite.
À 05:21:05 UTC, on observe Jupiter, sa hauteur instrumentale est 67°32'.
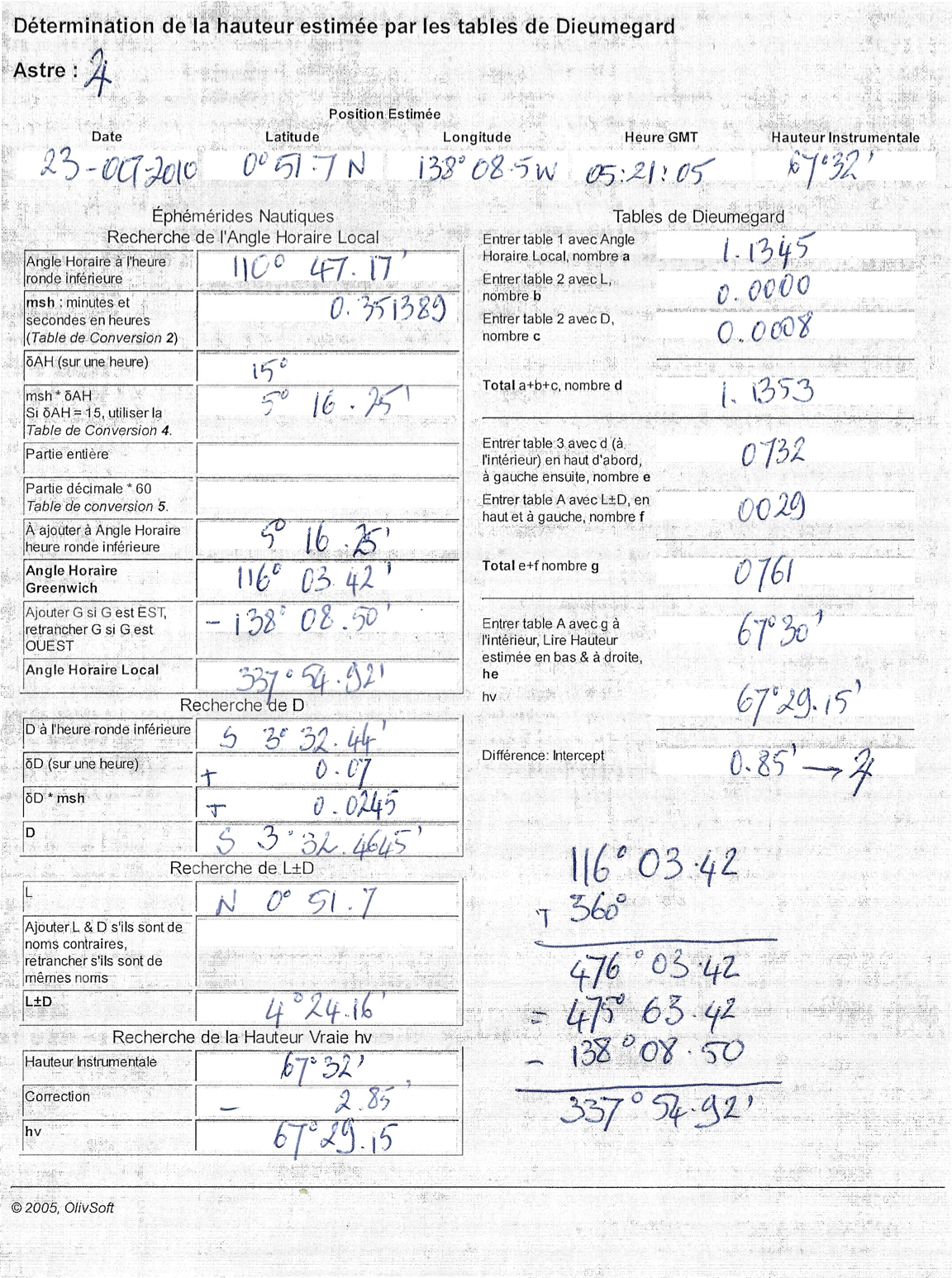
msh * δAH, comme la variation horaire (δAH) est de 15° (cette donnée vient des éphémerides), on utilise la table de correction 4 :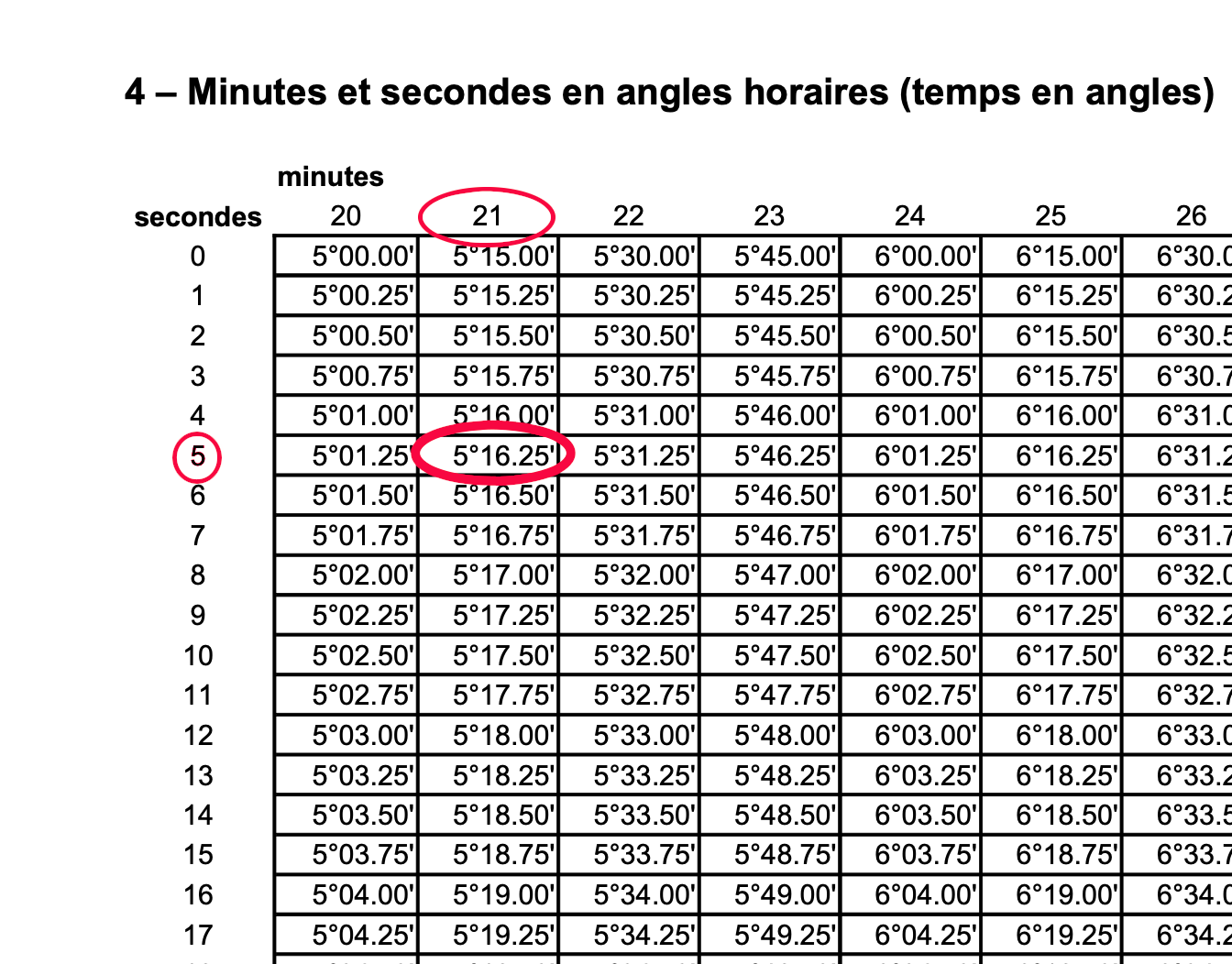
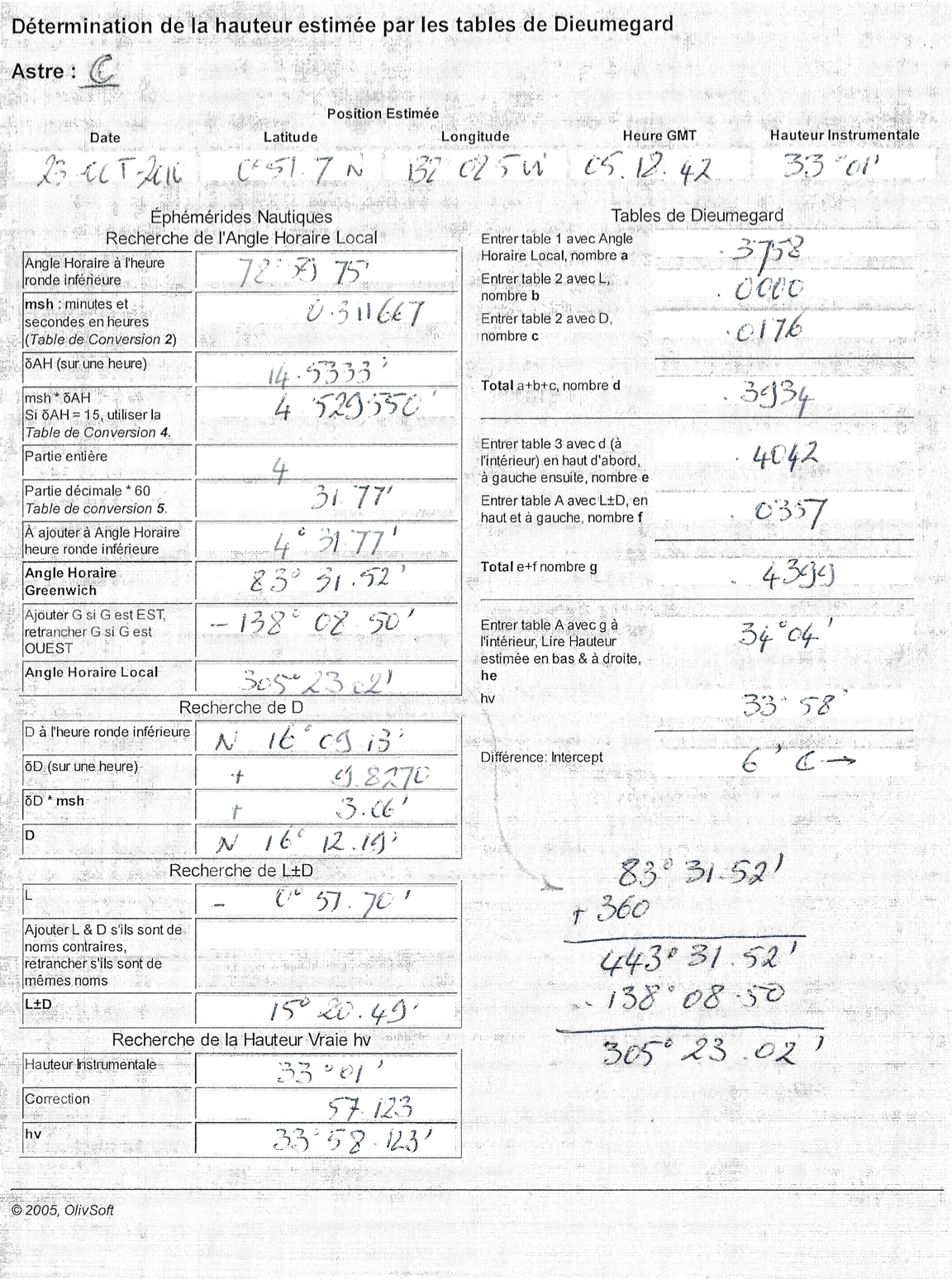
msh * δAH, comme la variation horaire n'est pas égale à 15°, on utilisera la table de correction 5 (ceux qui savent se passer de calculette vont être contents) :δAH = 14.5333°, et msh = 0.311667.msh * δAH = 14.5333 × 0.311667 = 4.5295500111° :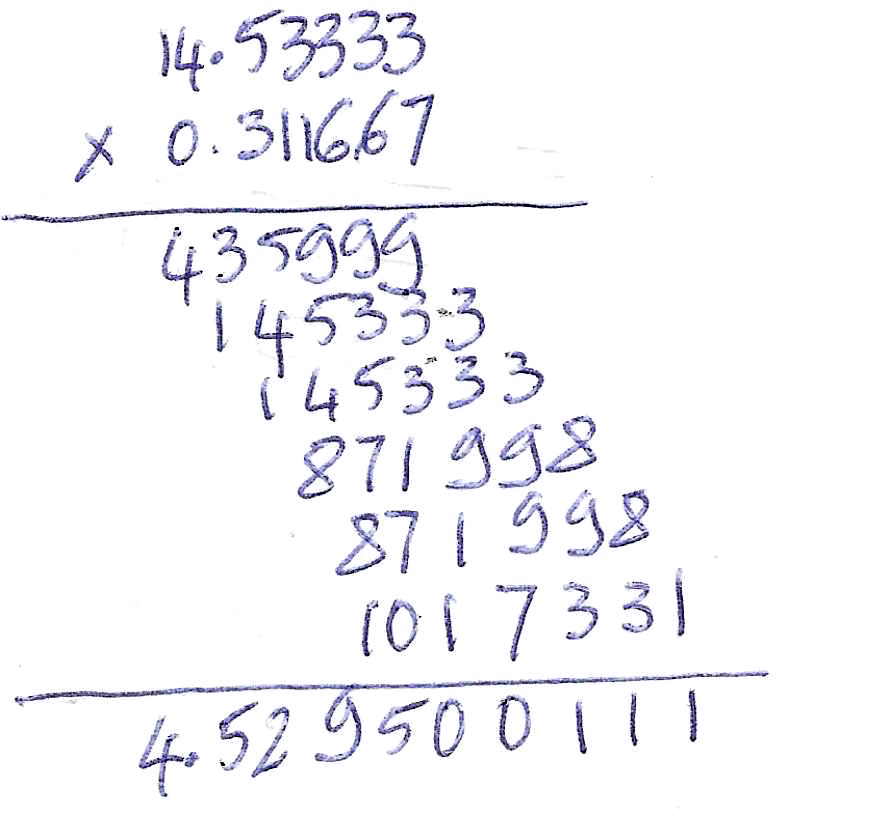
4.529550°.
0.529550 par 60, ou bien on la cherche dans la table 5 :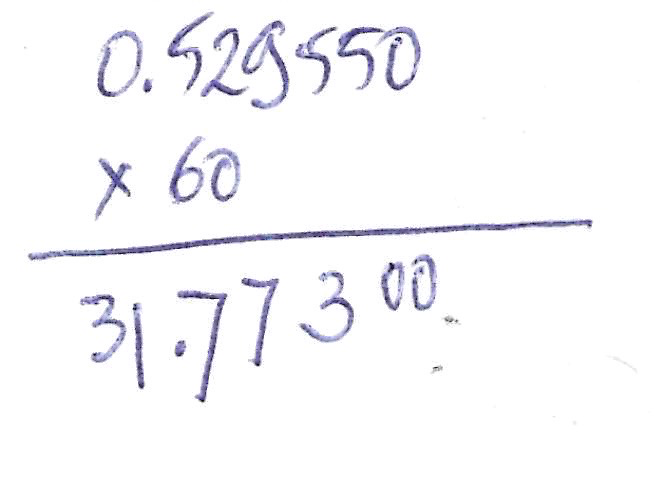
0.529550 dans la table 5 :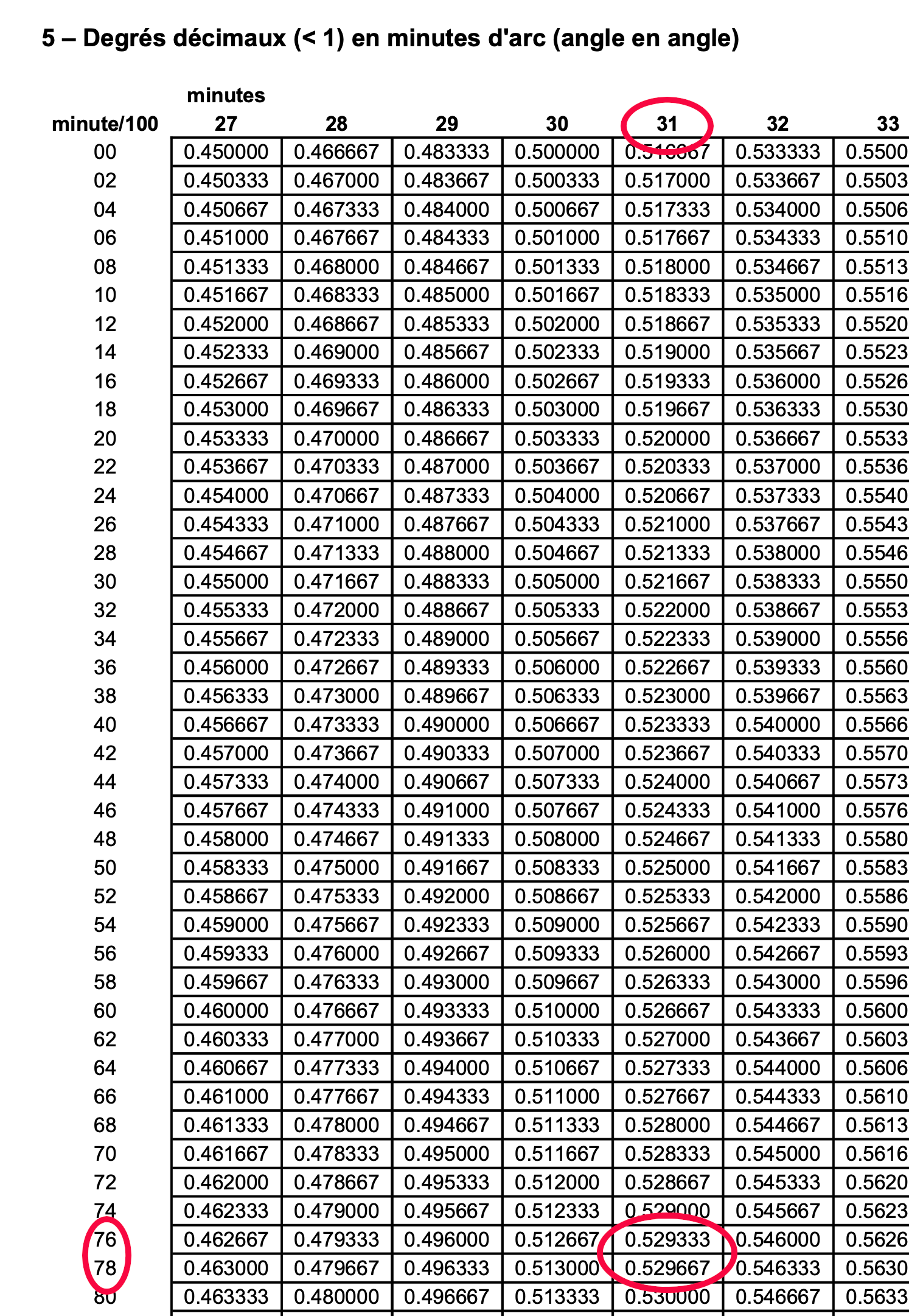
31, ligne 77, ce qui donne 31.77 !
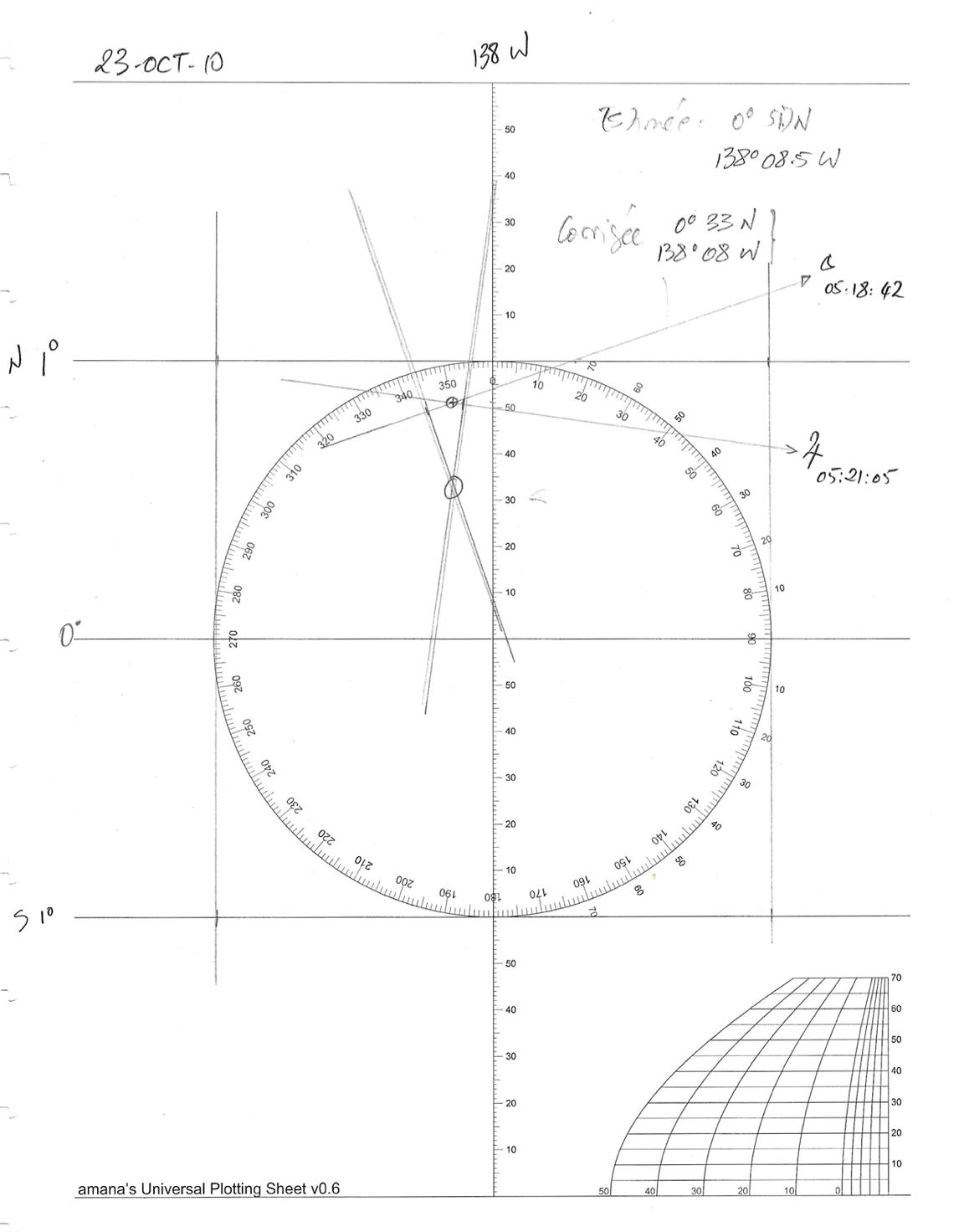
Le problème est ici de trouver les coefficients d'un polynôme de degré donné (choisi), afin que la courbe qui le représente soit aussi proche que possible d'un ensemble de points donnés.
Autrement dit, que la courbe trouvée colle autant que possible au nuage des points de départ.
|
$$
P^{HDC}_{COG} = P^x_y
$$
|
, écrit aussi |
$$
y = f(x)
$$
|
où |
$$
f(x) = ax^2 + bx + c
$$
|
a, b, c et d d'un polynôme pour lequel
y, c'est à dire que la différence
a, b et c pour lesquels la dérivée première de cette sommation des carrés des différences
par rapport à chacun des coefficients a, b et c est nulle, ce qui s'écrit :
a :
b :
c :
y de côté, on simplifie par 2, et on obtient la résolution matricielle suivante :
Pour un polynôme de degré n, le travail à effectuer se résume ainsi à inverser la matrice carrée $ \Sigma x^{0->2n} $ et de
la multiplier par la matrice colonne $ \Sigma yx^{0->n} $ pour obtenir la matrice ligne des coefficients du polynôme recherché.
On cherche ici à élaborer une courbe de déviation, à partir de points enregistrés depuis la station NMEA du bord.
Dans ce contexte, la station doit comporter un GPS, et un compas (compas électronique, donc). Le GPS permettra à la station NMEA de générer des chaînes RMC - qui vont contenir
la route fond (Course Over Ground, aka COG), le compas fournira à la station ce dont elle a besoin pour générer les Caps Compas (Heading, aka HDG, HDM, etc, suivant les stations).
Le fichier contenant les informations produites par la station NMEA aura ainsi une allure comme ceci :
. . .
$IIRMC,190402,A,0854.980,S,14006.028,W,00.0,008,031110,10,E,A*07
$IIVHW,,,126,M,00.0,N,,*61
$IIVLW,02839,N,000.0,N*53
$IIVWR,027,R,07.2,N,,,,*61
$IIDPT,012.3,+0.7,*40
$IIGLL,0854.979,S,14006.029,W,190403,A,A*56
$IIHDG,126,,,10,E*16
. . .
On note que le fichier peut contenir d'autres données (VHW, DPT, GLL, VLW, etc), qu'on ignorera ici.
[
{ "hdc": 210.000000, "dev": 4.000000 },
{ "hdc": 210.000000, "dev": 4.000000 },
{ "hdc": 210.000000, "dev": -1.000000 },
{ "hdc": 210.000000, "dev": -2.000000 },
{ "hdc": 208.000000, "dev": -4.000000 },
. . .
]
Plus de détails sur ces opérations sont disponibles dans d'autres documents :
r est le Cap Compas, dev est la déviation (δ entre HDC et HDM, cap compas et cap magnétique, voir ici).f pour laquelle la déviation dev est obtenue en fournissant r:
HDC (corrigé de la déclinaison locale)
et la route fond (COG) est bien la déviation d, que l'on cherche. Pas de dérive, pas de courant,
la route fond est égale à la route surface, qui est égale au
cap vrai du bateau (voir ici).
Pour les accros de la programmation:
Deux notebooks, pour l'azimuth et la hauteur estimée: